Question 833337: The cube of 99 is 970299. Consider the smallest two-digit number whose cube ends with the original two-digit number. The sum of the digits of the cube of that two-digit number is:
a) 18 b) 19 c)20 d)21 e)22
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Twelve-year old geniuses at the forum in the artofproblemsolving website may be able to provide a brilliant and concise explanation showing why choices b, c, d, and e are wrong. My explanation will not be so brilliant.
One strategy would be using a spreadsheet to have the computer calculate  and see if it ends in 00 for all numbers and see if it ends in 00 for all numbers  between 11 and 99. between 11 and 99.
Without using a computer, I need a different strategy.
Algebra tells me that
 . .
Since 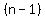 , ,  and and  are 3 consecutive numbers, all I need to do is look for 3 consecutive integers between 10 and 100 whose product ends in 00. are 3 consecutive numbers, all I need to do is look for 3 consecutive integers between 10 and 100 whose product ends in 00.
If the product ends in 00, it must be a multiple of  . .
Because the product is a multiple of  , one of the numbers must be a multiple of , one of the numbers must be a multiple of  , or else two of the numbers ( , or else two of the numbers ( 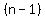 , and , and  ) must be even (multiples of ) must be even (multiples of  ). ).
Also, one of the 3 numbers must be a multiple of  , because we could not have two multiples of , because we could not have two multiples of  within the 3 consecutive integers. within the 3 consecutive integers.
So the products must include  , or , or  , or , or  or or  . .
For the smallest  , I should make , I should make  one of the 3 integers. one of the 3 integers.
The 3 consecutive integers including  would be smallest if we make would be smallest if we make  . In that case, for . In that case, for  to be a multiple of to be a multiple of  , we would need , we would need  (the only even integer of the three) to be a multiple of 4. (the only even integer of the three) to be a multiple of 4.
Since  means means  , ,  is the smallest two-digit number whose cube ends with the original two-digit number. is the smallest two-digit number whose cube ends with the original two-digit number.
Since  , ,  is a multiple of 9, and the sum of its digits must be a multiple of 9. It could not be 19, or 20, or 21, or 22. is a multiple of 9, and the sum of its digits must be a multiple of 9. It could not be 19, or 20, or 21, or 22.
If it is one of the options given, it must be  . .
|
|
|