SOLUTION: A circle is inscribed in a square which is in turn inscribed of a larger circle. what is the ratio of the area of the larger circle to that of the smaller circle? pls help me!

Algebra ->  Formulas -> SOLUTION: A circle is inscribed in a square which is in turn inscribed of a larger circle. what is the ratio of the area of the larger circle to that of the smaller circle? pls help me!       Log On


   

Question 832764: A circle is inscribed in a square which is in turn inscribed of a larger circle. what is the ratio of the area of the larger circle to that of the smaller circle?
pls help me!
Answer by math-vortex(648) About Me  (Show Source):
You can put this solution on YOUR website!
Hi, there--

THE PROBLEM:
A circle is inscribed in a square which is in turn inscribed of a larger circle. what is the ratio of the area of 
the larger circle to that of the smaller circle?

A SOLUTION:
You want the ratio of the area of the larger circle to that of the smaller circle.

Sandwiched between these two circles is a square. (See drawing below.)
We say that the smaller circle is inscribed in the square.
Likewise, the square is inscribed in the larger circle.




AREA OF SMALL CIRCLE
In order to find the area of a circle, we need to know its radius. Let's begin with the smaller circle. Do you
see that the radius of the smaller circle (AO) is one-half the side length of the square?

Let s be the side length of the square.
Then s/2 is the radius of the smaller circle.

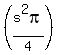An expression for the area of the smaller circle is pi%2Ar%5E2=pi%2A%28s%2F2%29%5E2 or %28s%5E2pi%2F4%29.

AREA OF LARGE CIRCLE
Now consider the larger circle. Do you see that the radius of this circle (OB) is one-half the diameter
of the square?

To find the diameter of the square, we use the Pythagorean Equation, a%5E2%2Bb%5E2=c%5E2.
The length and width of the square are the legs of a right triangle, the diagonal is the hypotenuse.

c%5E2=s%5E2%2Bs%5E2
c%5E2=2s%5E2

To find c, we take the square root of both sides of the equation.
c=sqrt%282s%5E2%29

Simplify. (The square root of c^2 is c, and the square root of s^2 is s.)
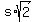c=s%2Asqrt%282%29

The length of the diagonal of the square is s%2Asqrt%282%29. The radius of the larger circle is half the length
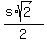of the diagonal, or %28s%2Asqrt%282%29%29%2F2.

An expression for the area of the larger circle is pi%2Ar%5E2=pi%2A%28%28s%2Asqrt%282%29%29%2F2%29%5E2.

We can simplify this expression. (The (sqrt(2))/2 squared is 2/4=1/2.)
pi%2A%28%28s%2Asqrt%282%29%29%2F2%29%5E2=%28pi%2As%5E2%29%2F2

RATIO OF AREAS
Let R be ratio of the area of the larger circle to the area of the smaller circle.

R=%28%28s%5E2%2Api%29%2F2%29%2F%28%28s%5E2%2Api%29%2F4%29

Simplify. The s^2 terms and pi cancel out.
R=%28%28cross%28s%5E2%2Api%29%29%2F2%29%2F%28%28cross%28s%5E2%2Api%29%29%2F4%29
R=%281%2F2%29%2F%281%2F4%29
R=2

The ratio of the area of the larger circle to the area of the smaller one is 2:1. In other words the larger 
circle has twice the area of the smaller one. Furthermore, since we use s for the side length of the square, 
we know that this ratio is true for a square of any side length.


Hope this helps! Feel free to email if you have any questions about the solution.

Good luck with your math,

Mrs. F
math.in.the.vortex@gmail.com