SOLUTION: Find sin(theta) and cos(theta) given that tan(theta) = 3. Do not use a calculator. I tried drawing triangles which terminate in the first and third quadrants (where tan is posit

I'll do the third quadrant part.  You can do the 1st quadrant part.

We draw an angle in the 3rd quadrant like below.  Since the tangent is the
opposite over the adjacent, or , we make the given tangent, 3, into a
fraction 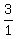, but x goes left and y goes down, so they both have to be
negative, so we change the 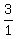 to  and make the numerator
-3 be the value of y and the denominator -1 be the value of x. 
{In the first quadrant they'll be positive].

so we have:    
 


Now we need to know that the sine is the opposite over the
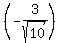hypotenuse or y/r, which is  or .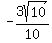 

And we need to know that the cosine is the adjacent over the
hypotenuse or x/r, which is  or . 

[Note: The sine and cosine are both negative in the third quadrant.  They will
be positive if the angle is taken in the first quadrant, because x and y
will both be positive there.  The value of r, the hypotenuse, or "radius
vector" is ALWAYS taken positive regardless of what quadrant it lies in.]

Edwin