Hi, there--
THE PROBLEM:
Use graphing to solve this system of equations:
y = 3x + 2
y = -x - 2
A SOLUTION:
When you use a graphing approach, you are going to make a graph with an x- and y-axis and plot the
graphs of these equations.
These happen to be two linear equations so their graphs will be lines. Except for two special cases (that
don't apply here), the solution to a system of linear equations is the point where the two lines intersect.
Your equations are both in slope-intercept form (y=mx+b). This makes them pretty easy to graph.
In slope-intercept form, the number in front of x (the x-coefficient) is the slope of the line. The constant
term to the far right, is the y-intercept.
The y-intercept is the place where the line crosses the y-axis (the vertical axis).
The slope tells you how steep the line is, the change in y divided by the change in x.
Look at the first equation, y = 3x + 2,
The slope is 3;
The y-intercept is 2.
For the second equation, y = -x - 2,
The slope is -1;
The y-intercept is -2.
Now we are ready to graph. Using graph paper, draw your x- and y-axes. Like this:
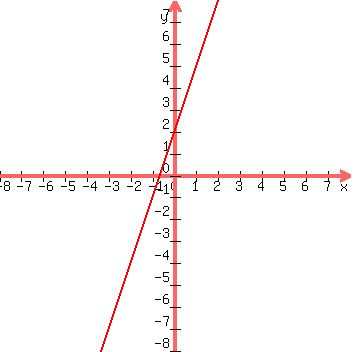
To graph the first equation, y = 3x + 2, find the point (0,2). This is the y-intercept. The line will cross the y-axis here. Mark this point.
The slope is 3. This means the line goes up 3 units for each step to the right.
Start at (0,2). Count up 3 units. Then count 1 unit to the right. Make a mark there at (1,5).
Repeat this one more time, starting at your secant point (up 3, right 1). Mark the point.
All three points you marks=ed are on the line. Use your ruler to carefully draw.
It should look like this:
Now we are ready to graph the second equation, y=-x - 2:
Mark at the y-intercept at (0,-2)
This time we have a slope of -1. When the slope is negative, the line goes down for each step to the right.
Starting at the y-intercept, count down 1, right one and mark the point (1, -3).
Repeat this several times because the points are so close together.
Your graph should look like this:
Solving by graphing is an estimating process. It looks like the interception point is very close to (-1, -1). This is the solution by graphing.
CHECK:
If you substitute x= -1 and y= -1 into both equations, you will see that this is a very good estimate.
y = 3x + 2
(-1) = 3(-1) + 2
-1 = -3 + 2
-1 = -1
TRUE
y = -x - 2
(-1) = -(-1) - 2
-1 = 1 - 2
-1 = -1
TRUE
The ordered pair (-1, -1) is exactly the solution to this system of equations.
Hope this helps! Feel free to email if you have ANY questions about the solution.
Good luck with your math,
Mrs. F
math.in.the.vortex@gmail.com
