SOLUTION: find sin theta if cos theta=1/2 and theta terminates in quadrant IV

Algebra ->  Trigonometry-basics -> SOLUTION: find sin theta if cos theta=1/2 and theta terminates in quadrant IV      Log On


   

Question 831646: find sin theta if cos theta=1/2 and theta terminates in quadrant IV
Found 2 solutions by stanbon, KMST:
Answer by stanbon(75887) About Me  (Show Source):
You can put this solution on YOUR website!
find sin theta if cos theta=1/2 and theta terminates in quadrant IV
-----
In QIV x is positive and y is negative
-------
Since cos = x/r, x = 1 and r = 2
Then y = -sqrt[2^2-1^2] = -sqrt(5)
-----
Ans: sin(t) = y/r = -sqrt(5)/2
=========================
Cheers,
Stan H.
=========================

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
For angles terminating in quadrant IV, sine is negative and cosine is positive.
For any angle theta , sin%5E2%28theta%29+%2B+cos%5E2%28theta%29=1 .
So, If cos%28theta%29=1%2F2 ,
sin%5E2%28theta%29+%2B+%281%2F2%29%5E2=1
sin%5E2%28theta%29+%2B+1%2F4=1
sin%5E2%28theta%29=1-1%2F4
sin%5E2%28theta%29=3%2F4
Since we know that 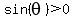sin%28theta%29%3E0 ,
sin%28theta%29=-sqrt%283%2F4%29 is not a solution.
The solution is
sin%28theta%29=sqrt%283%2F4%29
highlight%28sin%28theta%29=sqrt%283%29%2F2%29

NOTE:
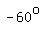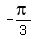We also know that one of the possible values of theta is -60%5Eo or -pi%2F3,
because a 30-60-90 right triangle (one with angles measuring 30, 60, and 90 degrees) is half of an equilateral triangle>

So for an equilateral triangle with side length of 1,
we get a right triangle where the leg opposite the 30%5Eo angle (adjacent to the 30%5Eo angle) measures 1%2F2 ,
meaning that sin%2830%5Eo%29=cos%2860%5Eo%29=1%2F2 .