SOLUTION: Please help me solve this expression; (xy+3)^2 x=2 y=5 This is what I have tried....(5)^2 x (2)^2 + 3 25 x 4 = 100+3=103

Algebra ->  Expressions -> SOLUTION: Please help me solve this expression; (xy+3)^2 x=2 y=5 This is what I have tried....(5)^2 x (2)^2 + 3 25 x 4 = 100+3=103       Log On


   

Question 831535: Please help me solve this expression; (xy+3)^2 x=2 y=5
This is what I have tried....(5)^2 x (2)^2 + 3
25 x 4 = 100+3=103
103 x 2 = 206
But the answer is 169...I want to understand how they got this answer so I can move on with my homework....Please help me understand...Thank you
Found 2 solutions by JulietG, KMST:
Answer by JulietG(1812) About Me  (Show Source):
You can put this solution on YOUR website!
(xy+3)^2
x=2
y=5
.
You didn't square the 3. Note that the square sign is OUTSIDE the parentheses.
.
[(2*5)+3]^2
[10+3]^2
13^2 = 169
.
Simple error. Otherwise you're fine.

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
When x=2 and y=5 xy means the product of x times y so xy=2%2A5 so xy=10 .
You probably knew that.
You may not quite remember the rules for order of operations, which may be a bit new to you.
To calculate %28xy%2B3%29%5E2=%282%2A5%2B3%29%5E2 , we have to calculate according to order of operation rules.
Those are the language rules of algebra that people have agreed to follow so that we can understand each other when we write out a calculation more complicated than what we used to do in 4th grade.
We need to calculate %282%2A5%2B3%29 before squaring it,
because there are parentheses around it, and parentheses are given first priority.
To calculate 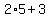2%2A5%2B3 we need to do the multiplication before the addition,
because multiplication has priority over addition.
So, in order, we calculate it like this:
%282%2A5%2B3%29%5E2=%2810%2B3%29%5E2 (multiplication done)
The next step is
%2810%2B3%29%5E2=13%5E2 (addition done, completing the calculation of the expression in parentheses)
The next and last step is
13%5E2=169
I could write the whole calculation in one line as
%282%2A5%2B3%29%5E2=%2810%2B3%29%5E2=13%5E2=169 ,
unless your teacher does not like to see it that way.

NOTES:
Many teachers do not like to see two equal signs in a row as in xy=2%2A5=10 or %282%2A5%2B3%29%5E2=%2810%2B3%29%5E2=13%5E2=169 .
They want to avoid having students write something wrong, like
25 x 4 = 100+3 = 103 .
When you wrote that you started with 25 x 4 = 100, which was true.
Then you thought about adding 3, and 100+3 = 103 is also true,
but when you added "+ 3" to the right of "25 x 4 = 100" you made it read
"25 x 4 = 100 + 3" and that is wrong.