Question 831418: a unit of tasks can be completed by A, B, C, D and E in 2 hours. If it is done by A and B, it can be completed in 4 hours 48 minutes, by B, C and D in 4 hours, and by A, C and E in 3 hours 12 minutes. How long does it take for each person to complete the unit of tasks?
Answer by AnlytcPhil(1806)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Check the problem again. A piece of information is missing.
There are 5 unknowns, but there is only enough information
to get 4 equations. That's called an "underdetermined" system.
(I'm assuming you're not taking linear algebra, or are you?
I'll assume you aren't.) We can at best get some of times,
and we may not get any! But let's see how far we can get
without the missing piece of information.
Let The answers be:
It takes A "a" hours to complete the task alone.
It takes B "b" hours to complete the task alone.
It takes C "c" hours to complete the task alone.
It takes D "d" hours to complete the task alone.
It takes E "e" hours to complete the task alone.
Then
A's working rate is 1 task per "a" hours or 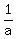 tasks/hour
B's working rate is 1 task per "b" hours or tasks/hour
B's working rate is 1 task per "b" hours or  tasks/hour
C's working rate is 1 task per "c" hours or tasks/hour
C's working rate is 1 task per "c" hours or 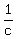 tasks/hour
D's working rate is 1 task per "d" hours or tasks/hour
D's working rate is 1 task per "d" hours or  tasks/hour
E's working rate is 1 task per "e" hours or tasks/hour
E's working rate is 1 task per "e" hours or  tasks/hour tasks/hour
a unit of tasks can be completed by A, B, C, D and E in 2 hours.
So their combined working rate is 1 task per "2" hours or  tasks/hour tasks/hour
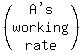  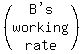  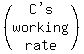  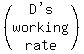  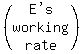  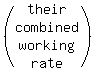 So
So
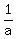    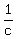       If it is done by A and B, it can be completed in 4 hours 48 minutes,
4 hours and 48 minutes is 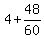 = = 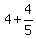 = = 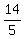 So their combined working rate is 1 task per
So their combined working rate is 1 task per 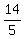 hours or hours or 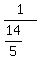 or or 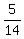 tasks/hour tasks/hour
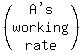  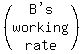  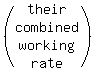
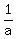    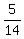 by B, C and D in 4 hours,So their combined working rate is 1 task per 4 hours or  tasks/hour. tasks/hour.
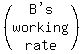  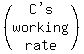  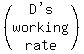  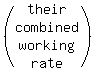
  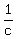     and by A, C and E in 3 hours 12 minutes.3 hours and 12 minutes is 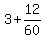 = = 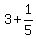 = =  So their combined working rate is 1 task per
So their combined working rate is 1 task per  hours or hours or 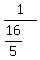 or or  tasks/hour tasks/hour
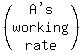  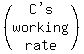  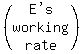  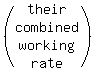
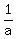  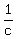     So we have the system of 4 equations in 5 unknowns;
So we have the system of 4 equations in 5 unknowns;
 We consider the reciprocals to be the variables and
make this 4×6 augmented matrix:
We consider the reciprocals to be the variables and
make this 4×6 augmented matrix:
 Using a TI graphing calculator I get the "rref":
Using a TI graphing calculator I get the "rref":
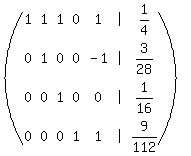 The third row translates as
The third row translates as
 , so c=16 and it takes C 16 hours to complete the task
So we substitute c=16 in the system , so c=16 and it takes C 16 hours to complete the task
So we substitute c=16 in the system
 and simplify
and simplify
 We'll put it in a 4×5 augmented matrix. But I'm quite
sure that will be a singular matrix.
We'll put it in a 4×5 augmented matrix. But I'm quite
sure that will be a singular matrix.
 And get the "rref"
And get the "rref"
 See? The bottom row is all 0's.
So the only answer we can get without the missing piece of
information is that C can complete the task in 16 hours.
Edwin
See? The bottom row is all 0's.
So the only answer we can get without the missing piece of
information is that C can complete the task in 16 hours.
Edwin
|
|
|