Question 831160: For which values of k does the equation x^-(4k+2)x+7k+2=0 form a perfect square ?
Answer by josgarithmetic(39614)   (Show Source):
You can put this solution on YOUR website! This description will not be the complete solution, but a description of how.
If you would Complete the Square for your given equation, put into Standard Form, you would obtain a constant term, which if were zero, would render your transformed, standard form equation, a perfect square. You would need to solve for k according to that "constant expression" being zero.
Note, our uses for "k" are different between your given equation and the usual generalized symbolism for showing how to Complete the Square.
See the lessons, "Completing the Square to Solve General Quadratic Equation" and
"What is Completing The Square? With Visual Explanation", found through the lessons link in my profile.
Tell me if you have further trouble with this.
-Requested Further Help-
------------------SOLUTION PROCESS---------------------------
Given  , what must be k so that the expression is a perfect square?
Complete the square for the  part, and perform other calculations on the other part of the given expression.
Square term to use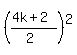 
We both ADD and SUBTRACT that square term!
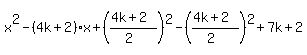
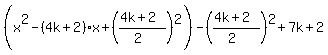
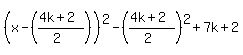
Very carefully see that this is a square expression PLUS a constant expression; and that k is a constant. We WANT that constant expression to be equal to zero. Symbolically this means we must have that:
If you understand all of this then, GOOD!
-
Reexplaining: The expression, 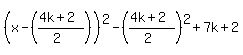, is not a square expression UNLESS 
-
Continuing to simplify that constant expression, I will omit the steps here, but it should transform into :
 .
Solve this for k.
-
Probably factorable, but resorting to general solution to quadratic formula,  or 
|
|
|
