Question 831122: A cylindrical jar of radius 3cm contains water to depth of 5cm. The water is then poured at a steady rate into an inverted conical container with its axis vertical. After t seconds, the depth of water in this container is x cm and the volume, V ml, of water that has been transferred is given by V= 1/3 (pie)(x)(x)(x).
Given that all the water is transferred in 3 seconds,find
a) dv/dt in terms of pie
b) the rate at which c is increasing at the moment when x= 2.5
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The volume in that cylindrical jar, calculated as 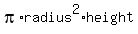 , ,
is  . .
a) If that volume is transferred at a steady rate in  minutes, the average and constant rate is minutes, the average and constant rate is
  (or (or 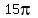 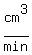 ). ).
b) Since there is no "c" mentioned in the problem before part b),
I assume that the question for part b) was
to find the rate (maybe called c) at which the water level is increasing in the inverted conical container,
when that water level there is  . .
That rate would be  . .
At a constant rate of 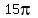  , at , at  minutes the volume in the inverted conical container would be minutes the volume in the inverted conical container would be 
We also know that  . .
We can use those two equations to find  and the value of and the value of  when when  . .
I believe the easiest way to find the value of  when when  is to consider that if is to consider that if  is a function of is a function of  and and  is a function of is a function of  , ,
 . .
We know that  (for all values of (for all values of  ), ),
and from  we calculate we calculate  . .
When  , ,  , ,
so at that point
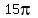 

 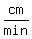
 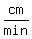 at the point when at the point when  . .
That does not give me a general expression for  as a function of as a function of  , but I do not believe the problem asked for that. , but I do not believe the problem asked for that.
However, just for fun, let's try to solve that way.
With your excuse, I will skip writting the units this time.
 --> -->  --> -->  --> -->  --> --> 


That still does not look pretty, but I cannot make improve it too much, so I let it be.
When  , ,  --> --> 
Substituting into  we get we get






So we get to the same result, and we have  as a function of as a function of  as a bonus, in exchange for a bit more arithmetic work. as a bonus, in exchange for a bit more arithmetic work.
|
|
|