|
Question 831056: In problems like (-31xm) + -2 =618 why do you bring the -2 over first? I can't figure out why sometimes it is the parenthesis and sometimes just the number. I thought it was order or operations but this doesn't seem to apply, it is not the parenthesis or the times part. It is the adding/subtracting you do first. How do you know????
Found 2 solutions by josgarithmetic, Edwin McCravy:
Answer by josgarithmetic(39620)   (Show Source):
You can put this solution on YOUR website! Your given equation has three terms:
-31xm;
-2;
618.
The grouping symbols around -31xm emphasise the grouped factors as a separate number from other numbers and symbols in the equation.
The variable term is -31xm. A person may want to solve for one or other of the variables contained in this term. Objective is to isolate the variable term, and finally one of the variables.
The left member contains -2.
We maintain equality between left and right members if we ADD THE ADDITIVE INVERSE OF -2 TO BOTH THE LEFT AND RIGHT MEMBERS.
-31xm+(-2)+2=618+2 ----- removing parentheses from -31xm causes no trouble; putting parentheses around -2 both emphasises that number and on this site will help with rendering.
-
-31xm+0=618+2 ----- Property and meaning of ADDITIVE INVERSE.
Answer by Edwin McCravy(20060)  (Show Source):
You can put this solution on YOUR website!
You're right that the order of operations for solving an equation
is not PEMDAS
1. Are there any parentheses? If so, remove them with the distributive property.
2. Are there any like terms? If so combine them.
3. Is there a constant terms on the left side? If, so, get it off
the left side and get its opposite on the right side.
4. Are there any like terms? If so, combine them.
5. Is there a variable term on the right side? Is so, get it off
the right side and get its opposite on the left side.
6. Are there any like terms? If so, combine them.
7. Is there only one variable term on the left and only one constant term on
the right? If so, and it's coefficient is not a fraction, divide both
sides by that coefficient. If the coefficient is a fraction, multiply
both sides by its reciprocal.
8. Cancel the coefficient on the left and simplify whats on the right.
Example:
3(x + 1) + 5x = 5(2x - 3) + 10.
1. Are there any parentheses? Yes, so we remove them with the distributive
property.
3x + 3 + 5x = 10x - 15 + 10
2. Are there any like terms? Yes so we combine them.
8x + 3 = 10x - 5
3. Is there a constant terms on the left side? Yes, there is a 3 on the
left side, so we get it off the left side and get its opposite on the right side.
8x = 10x - 5 - 3
4. Are there any like terms? Yes, so we combine them.
8x = 10x - 8
5. Is there a variable term on the right side? Yes, 10x. So we get it off
the right side and get its opposite on the left side.
8x - 10x = -8
6. Are there any like terms? Yes, so we combine them.
-2x = -8
7. Is there only one variable term on the left and only one constant term on
the right? If so, and it's coefficient is not a fraction? Yes so we divide
both sides by the coefficient -2 on the left.
  
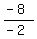8. We cancel the -2's on the left and simplify what's on the right to a
positive 4 because a negative divided by a negative is a positive
 
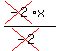x =
Sometimes the coefficient is a fraction, and when we get to step 7,
we multiply both sides by the reciprocal. Like this:
  
Then we multiply both sides by the reciprocal of the coefficient
which is 
Then we cancel on the left
 
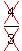x = 16
Edwin
|
|
|
| |
