Question 831042: Please help me solve this applying systems of linear equations word problem! Julie drove her car for 45 miles at an average speed of r miles per hour. On the return trip, traffic has increased, and Julie average speed is 3/4r. The round trip took a total of 1 hour and 45 minutes. Find the average speed for each portion of the trip. Thanks
Found 2 solutions by mananth, KMST:
Answer by mananth(16946)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I do not see that problem as an "applying systems of linear equations word problem", but I will try to do it that way, and also show you an alternate way.
THE MORE DIRECT WAY:
Average speed, time, and distance are related by
 <--> <-->  <--> <--> 
Measuring time in hours, it took  hours for the whole round trip. hours for the whole round trip.
The first part, at average speed  would have taken would have taken 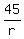 hours. hours.
The return trip, at average speed 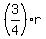 would have taken would have taken 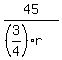 hours. hours.
Adding up, we get one equation.
or 
and we can solve for  . .
Solving:




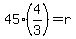
 and and 
USING SYSTEMS OF LINEAR EQUATIONS
 = time (in hours) Julie spent driving at an average speed of = time (in hours) Julie spent driving at an average speed of  miles per hour, while going wherever Julie was going. miles per hour, while going wherever Julie was going.
 = time (in hours) Julie spent driving at an average speed of = time (in hours) Julie spent driving at an average speed of 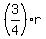 miles per hour during the return trip. miles per hour during the return trip.
Since  , for both parts of the trip we have , for both parts of the trip we have
 and and  , ,
and we could combine them into
 --> --> 
We also know that 
Solving:
 --> -->  --> -->  --> -->  --> --> 
So the average speed is  on the way over there, on the way over there,
and  for the return trip. for the return trip.
|
|
|