Question 830938: Find the rule of a quadratic function whose graph has the given vertex and passes through the given point.
Vertex (-1,-6) point (5,18)
Please help very confused.
Found 2 solutions by rothauserc, josmiceli:
Answer by rothauserc(4718)   (Show Source):
You can put this solution on YOUR website! the equation for a quadratic function with vertex (h, k) can be written as f(x)=a(x-h)^2+k.
The vertex of this function is (-1, -6), so once substituting that in, you have f(x)=a(x+1)^2 -6.
and then there is the point (5, 18) that the function passes through, so substitute 5 for x and 18 for f(x).
18 =a(5+1)^2 -6.
now solve for a,
18 =36a -6
36a = 24
a = 24/36 = 2/3
so this quadratic function is f(x)=2/3(x+1)^2 -6.
if you want it in the form f(x)=ax^2+bx+c, then multiply it out to get
f(x) = 2x^2/3 +4x/3 -16/3
Answer by josmiceli(19441)  (Show Source):
You can put this solution on YOUR website! The function is a parabola. If you plot
the given points, the vertex (-1,-6) is
in the 3rd quadrant, and (5,18) is in the
1st quadrant.
----------------------
It is important to see that the parabola
looks like a cup which is holding water
because the vertex is below the other
point
-----------------------
That means that the general form of the
equation is 
and 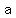 has to be positive for a parabola
that holds water.
------------------------
The formula for the vertex point is:
You are given  , so
------------------------
Also, I can plug the vertex point ( -1,-6)into the equation:
and, substituting for  ,
-------------------
So, now I have:
Now you can use the other given point, (5,18)
--------------
Then it follows that
and
--------------------
So, the equation is:
--------------------
check:
does it go through (-1,-6) ?
OK
-----------------------
Does it go through (5,18) ?
OK
-------
Hope this helps. Here's the plot:
|
|
|
