Question 83091: 1.) A tent opening is triangular in shape. The area of the opening is 12 square feet and the height is 48". What is the width of the bottom inches?
Next,.... 2.) A tent opening is triangular in shape. The area of the opening is 12 square feet and the bottom is 6 ft. What is the height of the opening in inches?
I really need help figuring out how to work these problems. Thanks.
Answer by chitra(359)  (Show Source):
You can put this solution on YOUR website! We know that the area of any triangle ]is given by :
A =  Where A = Area, b = base of the triangle, h = height of the triangle
According to the given data, Area = 12 sq ft, height = 48 ft
so, substituting in the formula, we get:
12 =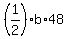 
==> 12 = b * 24
==> 
==> 
==> Therfore, the width of the bottom is 1/2 "
--------------------------------
================================
--------------------------------
Given area = 12 sq ft and the width of the bottom is 6 ft, to find the height of the triangle
Area =  * b * h
Substituting for the values, we get:
12 = * 6 * h
==> 12 = 3 * h
==>  = h
==> 4 = h
Hence, the height of the opening is 4 ft.
Thus, the solution..
HAPPY CALCULATING!!
|
|
|
