SOLUTION: the 3rd and 6th term of a geometric progression are 48 and 14 2/9 respectively. Write down the 1st 4 terms of the geometric progression.

a1, a2, a3=48, a4, a5, a6=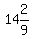

You need this formula for the nth term:

an = a1·r(n-1)

[Some books and teachers use "t" for "term" instead of "a".
I'll use "a".]

a3 = a1·r(3-1)
48 = a1·r2

a6 = a1·r(6-1)
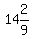 = a1·r5

Change 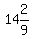 to an improper fraction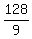 

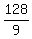 = a1·r5

Clear of fractions by multipolying both sides by 9

128 = 9a1·r5

So you have this system of equations:

 48 = a1·r2
128 = 9a1·r5

Solve the first for a1





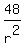
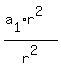
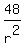
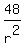 = a1

Substitute in

128 = 9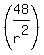·r5

128 =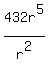 

Divide on the right by subtracting exponents:

128 = 432r³

Divide both sides by 432

 = 

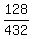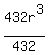Reduce the fraction on the left and cancel on the right:

 = 

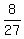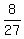 = r³

The cube root of 8 is 2 and the cube root of 27 is 3, so
taking cube roots of both sides:

 = r

Substitute for r in

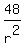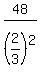 = a1

 = a1

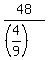 = a1 

To divide by a fraction, invert it and multiply

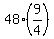 = a1

4 goes into 48 12 times:

 12
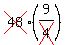 = a1
     1
 
108 = a1

1st term = ,
2nd term =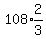 
3rd term =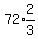 
4th term =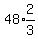 

the 3rd term checks, but to check the whole thing,
lets see if the 6th term is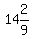 

5th term =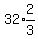 

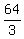
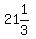6th term =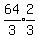 

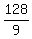
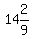So it checks.

Edwin