|
Question 830830: Solve Oblique conic : 10x2 +24xy + 17 y2 -9 = 0
1) Identify the conic. Explain your reasoning.
2.) Put the equation for the conic in standard form.
3.) State the Domain and Range of the Conic
4.) Graph the conic with foci, center, vertices, directrices, and asymptotes as needed for the conic. Be sure to label each element.
Found 3 solutions by stanbon, Edwin McCravy, KMST:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solve Oblique conic : 10x^2 +24xy + 17y^2 -9 = 0
Complete the square:
10(x^2 + 2.4xy + 1.2^2) + 17(y-0)^2 = 9 + 10*1.2^2
10(x+1.2)^2 + 17(y-0)^2 = 23.4
(x+1.2)^2/[23.4/10] + (y-0)^2/[23.5/17] = 1
---------
(x+1.2)^2/[1.52]^2 + (y-0)^2/1.18^2 = 1
=================================================
1) Identify the conic. Explain your reasoning.:: Ellipse
-------------------------------------------------------
2.) Put the equation for the conic in standard form.:: done
----------------------------------------------------------
3.) State the Domain and Range of the Conic
Since the center is at (-1.2,0)
Domain is [-1.2-1.52 , -1.2+1.52]
Range is [0-1.18 , 0+1.18]
-------------------------------------
4.) Graph the conic with foci, center, vertices, directrices, and asymptotes as needed for the conic. Be sure to label each element.
Comment: I'll leave these to you.
Cheers,
Stan H.
====================
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Since the other tutor gave you such a pitiful answer, I thought
I'd take the trouble to give you what you wanted. It's quite a
tough problem.
The general form of a conic is
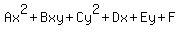  
   A=10, B=24, C=17
Discriminant B²-4AC = 24²-4(10)(17) = -104
This being negative tell us that the equation represents an
ellipse.
We will rotate the axes through an angle of
A=10, B=24, C=17
Discriminant B²-4AC = 24²-4(10)(17) = -104
This being negative tell us that the equation represents an
ellipse.
We will rotate the axes through an angle of  where where
  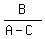  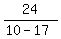  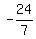
  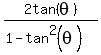
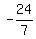  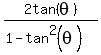 Let
Let  , then , then
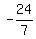  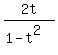 Divide both sides by 2
Divide both sides by 2
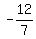  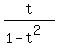
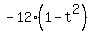  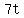
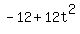  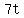
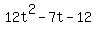  
  
 ; ;  We can choose either angle. I'll choose the positive one.
We can choose either angle. I'll choose the positive one.
 That's a 3-4-5 right triangle
That's a 3-4-5 right triangle  so
so  , , We make the substitution
We make the substitution
 , , 
 , ,  or
or
 , ,  [Most books use x' and y', but I am using capital X and Y because
primed letters are difficult to work with. So be careful in
the rest of the problem to distinguish between capital X and small x
and capital Y and small y. Remember the capital letters refer to the
rotated axes and small ones refer to the original un-rotated axes.]
Substitute into
[Most books use x' and y', but I am using capital X and Y because
primed letters are difficult to work with. So be careful in
the rest of the problem to distinguish between capital X and small x
and capital Y and small y. Remember the capital letters refer to the
rotated axes and small ones refer to the original un-rotated axes.]
Substitute into
  
  
   Multiply through by 25
10(3X-4Y)²+24(3X-4Y)(3Y+4X)+17(3Y+4X)²-225 = 0
10(9X²-24XY+16Y²)+24(9XY+12X²-12Y²-16XY)+17(9Y²+24XY+16X²)-225 = 0
90X²-240XY+160Y²+24(12X²-7XY-12Y²)+153Y²+408XY+272X²-225 = 0
90X²-240XY+160Y²+288X²-168XY-288Y²+153Y²+408XY+272X²-225 = 0
650X²+25Y²-225=0
Divide through by 25
26X²+Y²-9 = 0
To get that in standard form,
26X²+Y² = 9
Divide through by 9 to get 1 on the right
Multiply through by 25
10(3X-4Y)²+24(3X-4Y)(3Y+4X)+17(3Y+4X)²-225 = 0
10(9X²-24XY+16Y²)+24(9XY+12X²-12Y²-16XY)+17(9Y²+24XY+16X²)-225 = 0
90X²-240XY+160Y²+24(12X²-7XY-12Y²)+153Y²+408XY+272X²-225 = 0
90X²-240XY+160Y²+288X²-168XY-288Y²+153Y²+408XY+272X²-225 = 0
650X²+25Y²-225=0
Divide through by 25
26X²+Y²-9 = 0
To get that in standard form,
26X²+Y² = 9
Divide through by 9 to get 1 on the right
 Divide numerator and denominator of first term by 26
Divide numerator and denominator of first term by 26

 The center is the origin, because
The center is the origin, because
 can be written:
can be written:
 , and is of the form , and is of the form
 since 9=a²>b²= since 9=a²>b²=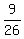 , and
where (h,k) is the center.
center = (X,Y) = (x,y) = (0,0)
a²=9, so a=3, so the (X,Y) coordinates of the vertex is on the Y-axis
is (X,Y) = (0,3). We translate this to its (x,y) coordinates, by using , and
where (h,k) is the center.
center = (X,Y) = (x,y) = (0,0)
a²=9, so a=3, so the (X,Y) coordinates of the vertex is on the Y-axis
is (X,Y) = (0,3). We translate this to its (x,y) coordinates, by using
 , , 
 , , 
 , ,  The upper left vertex is (x,y) = (
The upper left vertex is (x,y) = (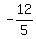 , , )
By symmetry, the lower right vertex is ( )
By symmetry, the lower right vertex is ( , ,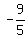 )
To find the foci, we need the value c,
c² = a²-b²
c² = 9- )
To find the foci, we need the value c,
c² = a²-b²
c² = 9-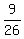 c² =
c² = 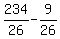 c² =
c² = 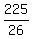 c =
c = 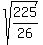 c =
c = 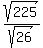 c =
c =  So the foci on the Y-axis are (X,Y) = (0,
So the foci on the Y-axis are (X,Y) = (0, )
We translate the one with the positive Y to its (x,y) coordinates, by using )
We translate the one with the positive Y to its (x,y) coordinates, by using
 , ,


 The upper left focus is (x,y) = (
The upper left focus is (x,y) = (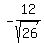 , ,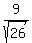 )
By symmetry, the lower right focus is ( )
By symmetry, the lower right focus is (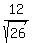 , ,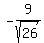 )
------------------
To find the domain and range exactly is really murder.
To find the range exactly
1. Solve the original equation for y using the quadratic formula
2. You will have two functions, one using + and one using -
3. Find their derivatives
4. Set each equal to 0 and solve for x
5. Substitute in the result of 1 to find y in each
6. The range will be [smaller value of y, larger value of y]
To find the domain exactly
1. Interchange x and y in the original equation.
2. Solve the that equation for y using the quadratic formula
3. You will have two functions, one using + and one using -
4. Find their derivatives.
5. Set each equal to 0 and solve for x
6. Substitute in the result of 2 to find y in each
7. The domain will be [smaller value of y, larger value of y]
That'll take many hours. I just used a TI-84 to find the
approximate domain and range,
The approximate domain is [-2.47386337,2.47386337]
The approximate range is [-2.283567,2.283567]
Edwin )
------------------
To find the domain and range exactly is really murder.
To find the range exactly
1. Solve the original equation for y using the quadratic formula
2. You will have two functions, one using + and one using -
3. Find their derivatives
4. Set each equal to 0 and solve for x
5. Substitute in the result of 1 to find y in each
6. The range will be [smaller value of y, larger value of y]
To find the domain exactly
1. Interchange x and y in the original equation.
2. Solve the that equation for y using the quadratic formula
3. You will have two functions, one using + and one using -
4. Find their derivatives.
5. Set each equal to 0 and solve for x
6. Substitute in the result of 2 to find y in each
7. The domain will be [smaller value of y, larger value of y]
That'll take many hours. I just used a TI-84 to find the
approximate domain and range,
The approximate domain is [-2.47386337,2.47386337]
The approximate range is [-2.283567,2.283567]
Edwin
Answer by KMST(5328)   (Show Source): (Show Source):
|
|
|
| |