Question 830810: Compound Interest. Suppose that $750 is invested at 7% interest, compounded semiannually.
a) Find the function for the amount to which the investment grows after t years.
b) Find the amount of money in the account at t=1,6,10,15, and 25 years.
Please help!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! a) 7% anual interest compounded semiannually means that every 6 months
 interest is added to the balance. interest is added to the balance.
That is  times the balance times the balance
After 6 months, you have
$ =$ =$ =$ =$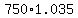 . .
You started with $750, but the calculation is the same for any other number.
In 6 months the amount grows by a factor of  . .
Six month later, at the 1 year mark, that $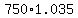 amount gets multiplied times amount gets multiplied times  again, again,
so after one year you have $ . .
That multiplication times  happens every year, so after happens every year, so after  years you have years you have
$ =$ =$
b) For  , the amount is , the amount is  (rounded). (rounded).
For  , the amount is , the amount is  (rounded). (rounded).
For  , the amount is , the amount is  (rounded). (rounded).
For  , the amount is , the amount is  (rounded). (rounded).
|
|
|