SOLUTION: Working together, three men can paint a barn in 6 hours. If each man worked alone, the first man would take twice as long the second, and the second would take six hours longer tha

Algebra ->  Problems-with-consecutive-odd-even-integers -> SOLUTION: Working together, three men can paint a barn in 6 hours. If each man worked alone, the first man would take twice as long the second, and the second would take six hours longer tha      Log On


   

Question 830661: Working together, three men can paint a barn in 6 hours. If each man worked alone, the first man would take twice as long the second, and the second would take six hours longer than the third. How many hours would it take the slowest man, working alone, to paint the barn?
Answer by josgarithmetic(39618) About Me  (Show Source):
You can put this solution on YOUR website!
Rates are best used in form and units of jobs per time.

ThreeTogether, 1/6 jobs per hour
manOne, ?
manTwo, ?
manThree, 1%2Fh, where h is the number of hours for him to do 1 job alone.
-
Work from manThree to get rate expressions for the other two men.
manTwo, 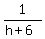1%2F%28h%2B6%29
manOne, 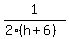1%2F%282%28h%2B6%29%29
-
The only variable, and unknown, is still h, the time for manThree to do this one job of painting the barn if he worked alone.

The sum of the men's individual rates is the rate for all three men working at the same time.
manOne%2BmanTwo%2BmanThree=ThreeTogether
highlight%281%2F%282%28h%2B6%29%29%2B1%2F%28h%2B6%29%2B1%2Fh=1%2F6%29
Solve for h in that highlighted equation. That will be the answer.