|
Question 83028: Solve the following system of linear inequalities by graphing.
x – y < 3
x + 2y >6
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Lets graph the equations first
 Simply replace the inequality sign with an equal sign Simply replace the inequality sign with an equal sign

So lets graph  first first
| Solved by pluggable solver: Graphing Linear Equations |
 Start with the given equation Start with the given equation
 Subtract Subtract 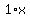 from both sides from both sides
 Multiply both sides by Multiply both sides by 
 Distribute Distribute 
 Multiply Multiply
 Rearrange the terms Rearrange the terms
 Reduce any fractions Reduce any fractions
So the equation is now in slope-intercept form ( ) where ) where  (the slope) and (the slope) and  (the y-intercept) (the y-intercept)
So to graph this equation lets plug in some points
Plug in x=-6

 Multiply Multiply
 Add Add
So here's one point (-6,-9)

Now lets find another point
Plug in x=-5

 Multiply Multiply
 Add Add
So here's another point (-5,-8). Add this to our graph

Now draw a line through these points
 So this is the graph of So this is the graph of  through the points (-6,-9) and (-5,-8) through the points (-6,-9) and (-5,-8)
So from the graph we can see that the slope is  (which tells us that in order to go from point to point we have to start at one point and go up 1 units and to the right 1 units to get to the next point) the y-intercept is (0, (which tells us that in order to go from point to point we have to start at one point and go up 1 units and to the right 1 units to get to the next point) the y-intercept is (0, )and the x-intercept is ( )and the x-intercept is ( ,0) . So all of this information verifies our graph. ,0) . So all of this information verifies our graph.
We could graph this equation another way. Since  this tells us that the y-intercept (the point where the graph intersects with the y-axis) is (0, this tells us that the y-intercept (the point where the graph intersects with the y-axis) is (0, ). ).
So we have one point (0, ) )

Now since the slope is  , this means that in order to go from point to point we can use the slope to do so. So starting at (0, , this means that in order to go from point to point we can use the slope to do so. So starting at (0, ), we can go up 1 units ), we can go up 1 units

and to the right 1 units to get to our next point

Now draw a line through those points to graph 
 So this is the graph of So this is the graph of  through the points (0,-3) and (1,-2) through the points (0,-3) and (1,-2)
|
Now lets graph 
| Solved by pluggable solver: Graphing Linear Equations |
 Start with the given equation Start with the given equation
 Subtract Subtract 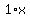 from both sides from both sides
 Multiply both sides by Multiply both sides by 
 Distribute Distribute 
 Multiply Multiply
 Rearrange the terms Rearrange the terms
 Reduce any fractions Reduce any fractions
So the equation is now in slope-intercept form ( ) where ) where  (the slope) and (the slope) and  (the y-intercept) (the y-intercept)
So to graph this equation lets plug in some points
Plug in x=-8

 Multiply Multiply
 Add Add
 Reduce Reduce
So here's one point (-8,7)

Now lets find another point
Plug in x=-6

 Multiply Multiply
 Add Add
 Reduce Reduce
So here's another point (-6,6). Add this to our graph

Now draw a line through these points
 So this is the graph of So this is the graph of  through the points (-8,7) and (-6,6) through the points (-8,7) and (-6,6)
So from the graph we can see that the slope is  (which tells us that in order to go from point to point we have to start at one point and go down -1 units and to the right 2 units to get to the next point), the y-intercept is (0, (which tells us that in order to go from point to point we have to start at one point and go down -1 units and to the right 2 units to get to the next point), the y-intercept is (0, )and the x-intercept is ( )and the x-intercept is ( ,0) . So all of this information verifies our graph. ,0) . So all of this information verifies our graph.
We could graph this equation another way. Since  this tells us that the y-intercept (the point where the graph intersects with the y-axis) is (0, this tells us that the y-intercept (the point where the graph intersects with the y-axis) is (0, ). ).
So we have one point (0, ) )

Now since the slope is  , this means that in order to go from point to point we can use the slope to do so. So starting at (0, , this means that in order to go from point to point we can use the slope to do so. So starting at (0, ), we can go down 1 units ), we can go down 1 units

and to the right 2 units to get to our next point

Now draw a line through those points to graph 
 So this is the graph of So this is the graph of  through the points (0,3) and (2,2) through the points (0,3) and (2,2)
|
So lets graph  and and  together together

Now lets pick the test point (0,0) and evaluate 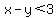
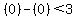
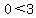 true. Shade the region that does contain (0,0) for true. Shade the region that does contain (0,0) for  . So this means you shade above the line . So this means you shade above the line 

Now lets use the same test point (0,0) and evaluate 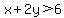
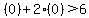
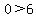 false. Shade the region that doesn't contain (0,0) for false. Shade the region that doesn't contain (0,0) for  . So this means you shade above the line . So this means you shade above the line 

Now the overlapping regions is the complete shading. In other words, every point that satisfies
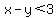
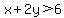
is in this region. So this is what the overlapped shaded region looks like:

|
|
|
| |