|
Question 82986This question is from textbook introductory algebra
: a mechanic requires 2 h to repair a tranmission, whereas an apprentice requires 6 h to make the same repairs. the mechanic worker alone for 1 h and then stopped. how long will it take the apprentice. working alone. to complete the repair?
This question is from textbook introductory algebra
Answer by Edwin McCravy(20056)   (Show Source):
You can put this solution on YOUR website!
A mechanic requires 2 h to repair a tranmission, whereas an apprentice
requires 6 h to make the same repairs. the mechanic worked alone for
1 h and then stopped. how long will it take the apprentice. working
alone. to complete the repair?
-----------------------------------------
This is a DRT problem, where "D" doesn't stand for "Distance", but
stands for "DEEDS DONE", or "fraction of a deed done". So make the
following chart. There are four situations to consider:
Deeds Rate Time
Mechanic doing 1 complete job
Apprentice doing 1 complete job
Mechanic doing partial job
Apprentice doing partial job
Let the answer to the question:
>>...How long will it take the apprentice. working alone. to complete the repair?...<<
be t. So fill in t for the time for the apprectice to do the partial
job of completing the job after the mechanic stops.
Deeds Rate Time
Mechanic doing 1 complete job
Apprentice doing 1 complete job
Mechanic doing partial job
Apprentice doing partial job t
-------------------------------------
>>..A mechanic requires 2 h to repair a tranmission..<<
That's 1 deed in 2 hours, so fill in 1 deed and 2 hours on
the top row:
Deeds Rate Time
Mechanic doing 1 complete job 1 2
Apprentice doing 1 complete job
Mechanic doing partial job
Apprentice doing partial job t
-------------------------------------
>>..an apprentice requires 6 h to make the same repairs..<<
That's 1 deed in 6 hours, so fill in 1 deed and 2 hours on
the second row:
Deeds Rate Time
Mechanic doing 1 complete job 1 2
Apprentice doing 1 complete job 1 6
Mechanic doing partial job
Apprentice doing partial job t
--------------------------------------
Next we use the formula R = 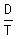 to fill in the rates
on the two top lines:
Deeds Rate Time
Mechanic doing 1 complete job 1 1/2 2
Apprentice doing 1 complete job 1 1/6 6
Mechanic doing partial job
Apprentice doing partial job t
--------------------------------------
Now, since the mchanic and the apprentice doing the partial
jobs work at the same rates as when they do 1 complete job,
we can fill in  and  for the rates in the bottom two
rows:
Deeds Rate Time
Mechanic doing 1 complete job 1 1/2 2
Apprentice doing 1 complete job 1 1/6 6
Mechanic doing partial job 1/2 1
Apprentice doing partial job 1/6 t
------------------------------------------
Next we use the formula D = RT to finish filling in the chart:
Deeds Rate Time
Mechanic doing 1 complete job 1 1/2 2
Apprentice doing 1 complete job 1 1/6 6
Mechanic doing partial job 1/2 1/2 1
Apprentice doing partial job t/6 1/6 t
Now that the chart is complete, we form the equation by observing
the partial job which the mechanic did + the partial job which the apprentice
did = 1 complete job:
1/2 + t/6 = 1
Can you solve that? If not post again asking how.
Answer: t = 3 hours.
Actually you can check it easy because you can do the whole
thing in your head by looking at it this way. The mechanic
does a whole job in 2 hours. So in the one hour he worked,
he did half the job. That leave the other half of the job to
be done by the apprentice. The apprentice can do a whole job
in 6 hours, so he can do the remaining half-job which the
mechanic left him with in half that time, or 3 hours.
Edwin
|
|
|
| |
