|
Question 829415: find the equation of the line through (7,-4) passing at a distance 1 from the point (2,1)
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website!
We will use the point-to-line formula:
The perpendicular distance from the point (x1,y1)
to the line Ax+By+C=0 is
d =  Suppose the required line has the equation
y = mx+b
Since it passes through (7,-4)
-4 = m(7)+b
-4 = 7m + b
-4-7m = b
So y = mx+b becomes
y = mx-4-7m
Let's get it in the form Ax+By+C=0 so we can use
the point-to-line formula above.
mx-4-7m = y
mx-y-4-7m = 0
where A = m, B=-1, C=-4-7m
Using the point-to-line formula
d =
Suppose the required line has the equation
y = mx+b
Since it passes through (7,-4)
-4 = m(7)+b
-4 = 7m + b
-4-7m = b
So y = mx+b becomes
y = mx-4-7m
Let's get it in the form Ax+By+C=0 so we can use
the point-to-line formula above.
mx-4-7m = y
mx-y-4-7m = 0
where A = m, B=-1, C=-4-7m
Using the point-to-line formula
d =  Since we want d to equal 1, and (x1,y1) = (2,1)
1 =
Since we want d to equal 1, and (x1,y1) = (2,1)
1 = 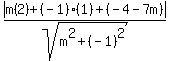 1 =
1 = 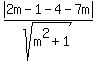 1 =
1 = 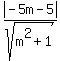 Multiply both sides by
Multiply both sides by 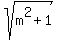
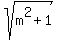  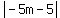 Square both sides
m²+1 = (-5m-5)²
m²+1 = (-5m-5)(-5m-5)
m²+1 = 25m²+25m+25m+25
m²+1 = 25m²+50m+25
0 = 24m²+50m+24
Divide through by 2
0 = 12m²+25m+12
0 = (4m+3)(3m+4)
Use the zero-factor property:
4m+3=0 3m+4=0
4m=-3 3m=-4
m=
Square both sides
m²+1 = (-5m-5)²
m²+1 = (-5m-5)(-5m-5)
m²+1 = 25m²+25m+25m+25
m²+1 = 25m²+50m+25
0 = 24m²+50m+24
Divide through by 2
0 = 12m²+25m+12
0 = (4m+3)(3m+4)
Use the zero-factor property:
4m+3=0 3m+4=0
4m=-3 3m=-4
m= m= m= So we have two solutions. From above we have
-4-7m = b
Using m=
So we have two solutions. From above we have
-4-7m = b
Using m= -4-7(
-4-7( ) = b
-4+( ) = b
-4+( ) = b
Clear of fractions:
-16+21 = 4b
5 = 4b ) = b
Clear of fractions:
-16+21 = 4b
5 = 4b
 = b
Substituting in y = mx+b = b
Substituting in y = mx+b
  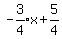 That's one solution.
Using m=
That's one solution.
Using m= -4-7(
-4-7( ) = b
-4+( ) = b
-4+(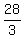 ) = b
Clear of fractions:
-12+28 = 3b
16 = 3b ) = b
Clear of fractions:
-12+28 = 3b
16 = 3b
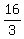 = b
Substituting in y = mx+b = b
Substituting in y = mx+b
  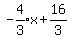 Now let's draw the graphs and see if it looks right. We plot the points
(2,1) and (7,-4) and the lines
Now let's draw the graphs and see if it looks right. We plot the points
(2,1) and (7,-4) and the lines
  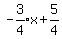
  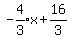
 Those lines both pass through (7,-4) and they look like they are both
1 unit from the point (2,1). So that must be correct
Edwin
Those lines both pass through (7,-4) and they look like they are both
1 unit from the point (2,1). So that must be correct
Edwin
|
|
|
| |