y = 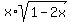 at the point (-4,-12)
The derivative is the slope of the tangent line.
The slope of the normal is the negative reciprocal of
the slope of the tangent line.
So.
1. We find the derivative.
2. We substitute x=-4 and simplify
3. We take the negative reciprocal of the result of 2
4. We use the point-slope formula with this slope and the given point.
at the point (-4,-12)
The derivative is the slope of the tangent line.
The slope of the normal is the negative reciprocal of
the slope of the tangent line.
So.
1. We find the derivative.
2. We substitute x=-4 and simplify
3. We take the negative reciprocal of the result of 2
4. We use the point-slope formula with this slope and the given point.


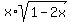
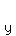

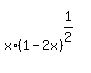


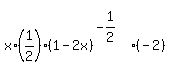
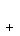
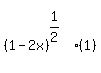



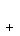
 We substitute x=-4
We substitute x=-4


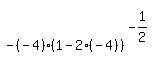
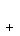
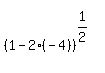


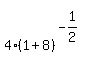
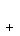
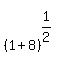


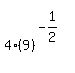
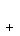
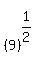


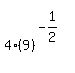
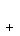
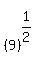



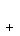



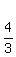
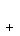
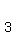


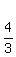
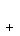
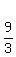


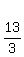 The slope of the tangent line is
The slope of the tangent line is 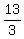 , so the slope of the
normal is
, so the slope of the
normal is 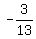 So we want the equation of the line through (-4,-12) with slope
So we want the equation of the line through (-4,-12) with slope 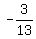 y - y1 = m(x - x1)
where (x1,y1) = (-4,-12)
y - y1 = m(x - x1)
where (x1,y1) = (-4,-12)


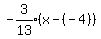
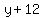

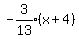 Multiply through by 13
13y+156 = -3(x+4)
13y+156 = -3x-12
3x+13y = -168
Here's the graph, it looks like a normal (perpendicular) line.
So it must be correct.
Multiply through by 13
13y+156 = -3(x+4)
13y+156 = -3x-12
3x+13y = -168
Here's the graph, it looks like a normal (perpendicular) line.
So it must be correct.
 Edwin
Edwin