|
Question 828701: The sides of a triangle all have integral measure and can be represented by the expressions x + 10, 2x -3, and 4x. For how many values of x will the sum of the two longer sides be divisible by the shortest side?
Found 2 solutions by math-vortex, Edwin McCravy:
Answer by math-vortex(648)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi, there--
THE PROBLEM:
The sides of a triangle all have integral measure and can be represented by the expressions x
+ 10, 2x -3, and 4x. For how many values of x will the sum of the two longer sides be
divisible by the shortest side?
A SOLUTION:
The triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than the length of the remaining side.
We have 3 situations that must all be true.
I. x + 10 < (2x - 3) + (4x)
II. 2x-3 < (x + 10) + (4x)
III. 4x < (x + 10) + (2x - 3)
CASE I:
x + 10 < 2x - 3 + 4x
x + 10 < 6x - 3
x < 6x - 13
-5x < -13
x > 13/5 (Remember to reverse the direction of the inequality.)
CASE II:
2x - 3 < x + 10 + 4x
2x - 3 < 5x + 10
-3x - 3 < 10
-3x < 10 + 3
-3x < 13
x > 13/-3 (Reverse inequality.)
x > -13/3
CASE III:
4x < 2x - 3 + 10 + 4x
4x < 3x + 7
x < 7
Now we combine the information from each inequality Recall that the sides of this triangle
have integral measure. Also, because it is the side length of the triangle.
x > 5/13 AND x > -13/3 ANG x < 7
x must be an integer such that x>13/5, so x = 3, 4, 5…
AND
x is an integer such that x>-13/3, so x = 1, 2, 3,…
AND
x is an integer such that x<7, so x = 1, 2, 3, 4, 5, 6, 7
Taken together, we see that must equal 3, 4, 5, or 6 in order for the triangle to exist.
For which values of x will the sum of the longer sides be divisible by the shortest side?
When x = 3,
x + 10 = 13
2x - 3 = 3
4x = 12
The sum of the longer sides is 25 which is not divisible by 3.
When x = 4,
x + 10 = 14
2x - 3 = 5
4x = 16
The sum of the longer sides is 30 which is divisible by 5.
When x = 5,
x + 10 = 15
2x - 3 = 7
4x = 20
The sum of the longer sides is 35 which is divisible by 7
When x = 6,
x + 10 = 16
2x - 3 = 9
4x = 24
The sum of the longer sides is 40 which is not divisible by 9.
For two values, x=4 and x=5, the sum of the longer sides is divisible by the shorter side.
Interesting problem. I hope this helps! Feel free to email if you have any questions about the
solution.
Good luck with your math,
Mrs. F
math.in.the.vortex@gmail.com
Answer by Edwin McCravy(20062)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Since the sides must be positive integers,
4x will always be greater than 2x-3.
So we have three cases to consider:
Case 1: 

 Since these are the sides of a triangle, the sum of the
two shorter sides must by greater than the longest side
Since these are the sides of a triangle, the sum of the
two shorter sides must by greater than the longest side
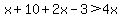

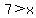 So there are no solutions in case 1, since those
inequalities contradict each other.
Case 2:
So there are no solutions in case 1, since those
inequalities contradict each other.
Case 2: 
 and and 
 and and 

 Since these are the sides of a triangle, the sum of the
two smaller sides must be greater than the largest side
Since these are the sides of a triangle, the sum of the
two smaller sides must be greater than the largest side
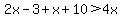

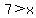
 So we have the possibility
So we have the possibility  For x=4
For x=4 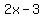 , ,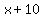 , , 2x-3=2(4)-3=8-3=5
x+10=4+10=14
4x=4(4)=16
The sides are 5,14,16
The sum of the two longer sides is 30, which
is divisible by the shortest side, 5.
So one solution is x=4
For x=5
2x-3=2(4)-3=8-3=5
x+10=4+10=14
4x=4(4)=16
The sides are 5,14,16
The sum of the two longer sides is 30, which
is divisible by the shortest side, 5.
So one solution is x=4
For x=5 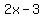 , ,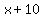 , , 2x-3=2(5)-3=10-3=7
x+10=5+10=15
4x=4(5)=20
The sides are 7,15,20
The sum of the two longer sides is 35, which
is divisible by the shortest side, 7.
So a second solution is x=5
For x=6
2x-3=2(5)-3=10-3=7
x+10=5+10=15
4x=4(5)=20
The sides are 7,15,20
The sum of the two longer sides is 35, which
is divisible by the shortest side, 7.
So a second solution is x=5
For x=6 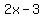 , ,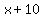 , , 9,16,24
The sum of the two longer sides is 40, which
is NOT divisible by the shortest side, 9. So x=6
is NOT a solution.
So from case 1, we have exactly two solutions, x=4 and x=5
Case 3:
9,16,24
The sum of the two longer sides is 40, which
is NOT divisible by the shortest side, 9. So x=6
is NOT a solution.
So from case 1, we have exactly two solutions, x=4 and x=5
Case 3: 



 Since these are the sides of a triangle, the sum of the
two shorter sides must be greater than the longest side
Since these are the sides of a triangle, the sum of the
two shorter sides must be greater than the longest side
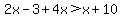
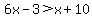


 So we have one possibility x=3
So we have one possibility x=3
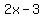 , , , ,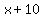 2x-3=2(3)-3=6-3=3
4x=4(3)=12
x+10=3+10=13
The sides are 3,12,13
The sum of the two longer sides is 25, which
is NOT divisible by the shortest side, 3. So x=3
is NOT a solution.
------------
This exhausts all the possibilities, so the answer is
There are exactly two possibilities:
x=4 which yields sides 5, 14, 16
x=5 which yields sides 7, 15, 20
Edwin
2x-3=2(3)-3=6-3=3
4x=4(3)=12
x+10=3+10=13
The sides are 3,12,13
The sum of the two longer sides is 25, which
is NOT divisible by the shortest side, 3. So x=3
is NOT a solution.
------------
This exhausts all the possibilities, so the answer is
There are exactly two possibilities:
x=4 which yields sides 5, 14, 16
x=5 which yields sides 7, 15, 20
Edwin
|
|
|
| |