SOLUTION: What is the sequence to 2 7 22 67 202

2 7 22 67 202

Each term is 1 more than 3 times the preceding term.

A recursive rule would be "to get the next term, multiply the previous term
by 3 then add 1": 

, 

But let's see if we can get the general term:

We make the sequences of differences between successive 
terms to see if they follow a pattern

  2    7-2 =   5 = 5×30
  7   22-7 =  15 = 5×31
 22  67-22 =  45 = 5×32
 67 202-67 = 135 = 5×33
202

1st term = 2
2nd term = 2+5×30 = 7
3rd term = 2+5×30+5×31 = 22
4th term = 2+5×30+5×31+5×32 = 67
5th term = 2+5×30+5×31+5×32+5×33 = 202

We see a pattern and we would suppose that the next term is

6th term = 2+5×30+5×31+5×32+5×33+5×34 = 607

So we assume that the general term is:

kth term = 2+5×30+5×31+5×32+···+5×3k-2

or factoring 5 out of all those with factor 5:

kth term = 2+5(30+31+32+···+3k-2)

The terms in parentheses is the sum of a geometric sequence with 
=1, =3k-2,  r=3,   

Sn =  

 =  =  =  = 

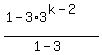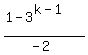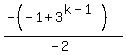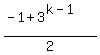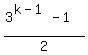Now let's go back the the general term 

kth term = 2+5(30+31+32+···+3k-2)

and substitute for the terms in the parentheses:

kth term = 2+5 =  =  =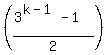 
 =  = 

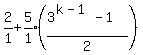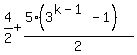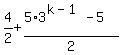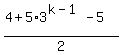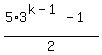So if you want to call it the nth term instead of the kth term, just
use n instead of k:



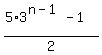You can crank out as many terms as you like.  Here are the first 20:

2, 7, 22, 67, 202, 607, 1822, 5467, 16402, 49207, 147622, 442867, 1328602,
3985807, 11957422, 35872267, 107616802, 322850407, 968551222, 2905653667.

Edwin