Question 82850: when using the quadratic formula to solve a quadratic equation (ax^ + bx + c = 0), the discriminant is b2 - 4ax. This discriminant can be positive, zero, or negative.
Create three unique equations where the discriminat is positive, zero, or negative. For each case, explain what this value means to the graph of y = ax^ + bx + c.
Answer by Edwin McCravy(20056)   (Show Source):
You can put this solution on YOUR website! when using the quadratic formula to solve a quadratic equation (ax^ + bx + c = 0), the discriminant is b2 - 4ax. This discriminant can be positive, zero, or negative.
Create three unique equations where the discriminat is positive, zero, or negative. For each case, explain what this value means to the graph of y = ax^ + bx + c.
Case 1.
y = x² + x - 2
a = 1, b = 1, c = -2
Discriminant = b² - 4ac = (1)² - 4(1)(-2) = 1 + 8 = 9
The discriminant 9 is positive so it has two real zeros
Here is the graph:
Its two real zeros are -2 and 1, the x-values at the two
points where the graph crosses the x-axis.
Case 2.
y = 4x² - 4x + 1
a = 4, b = -4, c = 1
Discriminant = b² - 4ac = (-4)² - 4(4)(1) = 16 + 16 = 0
The discriminant is zero so it has only one real zero.
Here is the graph:
Its one real zero is at 1/2, the x-value where the graph
just touches the x-axis. We say it is tangent to
the x-axis at that one point.
Case 3.
y = x² + x + 1
a = 1, b = 1, c = 1
Discriminant = b² - 4ac = (1)² - 4(1)(1) = 1 - 4 = -3
The discriminant -3 is negative so it has no real zeros.
Here is the graph:
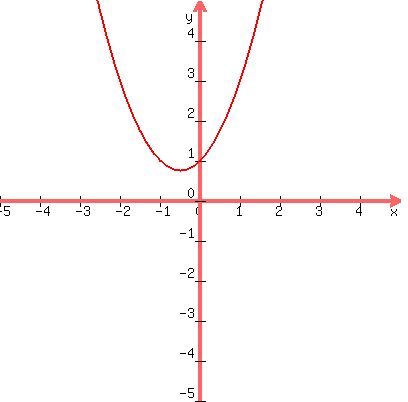It does not cross or touch the x-axis at all, so there
are no real zeros.
Edwin
|
|
|
