Question 82845: using the exact values find the numerical value of
a. sin 30degrees cos 240degrees + sin 210degrees sin 300degrees
b. tan 225degrees + tan (-45degrees)
Found 2 solutions by stanbon, funmath:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! using the exact values find the numerical value of
a. (sin 30degrees)( cos 240degrees) + (sin 210degrees)(sin 300degrees)
(1/2)(-1/2) + (-1/2)(-sqrt3/2)
= (1/4) - (sqrt3)/4)
-(1 - sqrt3)/4
==========================
b. tan 225degrees + tan (-45degrees)
= 1 + -1 = 0
==================
cheers,
Stan H.
Answer by funmath(2933)   (Show Source): (Show Source):
You can put this solution on YOUR website! using the exact values find the numerical value of
a. sin 30degrees cos 240degrees + sin 210degrees sin 300degrees
sin 30=1/2
:
cos 240 is in QIII, so it's negative and has a reference angle of 240-180=60, cos 60=1/2, therefore the cos 240=-1/2
:
sin 210 is in QIII, so it's negative and has a reference angle of 210-180=30, sin 30=1/2, therefore sin 210=-1/2
sin 300 is in QIV, so it's negative and has a reference angle of 360-300=60, sin 60=sqrt(3)/2, therefore sin 300=-sqrt(3)/2


:
b. tan 225degrees + tan (-45degrees)
tan 225 is in QIII which is positive for tan and has a reference angle of 225-180=45, tan 45 = 1, therefore tan 225=1
:
tan -45 is in QIV which is negative for tan and has a reference angel of 45, tan 45 =1 , therefore tan -45=-1
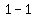

Happy Calculating!!!
|
|
|