|
Question 82830: write the standard form of the equation:
through (-1,-3) perpendicular to y=-1/5x +5
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Since the slope of the given line is  , the perpendicular slope is the negative reciprocal of the given slope. So the perpendicular slope is , the perpendicular slope is the negative reciprocal of the given slope. So the perpendicular slope is  or just 5. or just 5.
So lets find the equation of the line with a slope of 5 and goes through (-1,-3)
| Solved by pluggable solver: FIND a line by slope and one point |
What we know about the line whose equation we are trying to find out:
- it goes through point (-1, -3)
- it has a slope of 5
First, let's draw a diagram of the coordinate system with point (-1, -3) plotted with a little blue dot:

Write this down: the formula for the equation, given point  and intercept a, is and intercept a, is
 (see a paragraph below explaining why this formula is correct) (see a paragraph below explaining why this formula is correct)
Given that a=5, and  , we have the equation of the line: , we have the equation of the line:

Explanation: Why did we use formula  ? Explanation goes here. We are trying to find equation y=ax+b. The value of slope (a) is already given to us. We need to find b. If a point ( ? Explanation goes here. We are trying to find equation y=ax+b. The value of slope (a) is already given to us. We need to find b. If a point ( , , 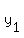 ) lies on the line, it means that it satisfies the equation of the line. So, our equation holds for ( ) lies on the line, it means that it satisfies the equation of the line. So, our equation holds for ( , , 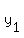 ): ):  Here, we know a, Here, we know a,  , and , and 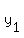 , and do not know b. It is easy to find out: , and do not know b. It is easy to find out:  . So, then, the equation of the line is: . So, then, the equation of the line is:  . .
Here's the graph:

|
|
|
|
| |