SOLUTION: hi! can u help me with these questions.? thank u! (applications of the derivative) 1) after x weeks, the number of people(or population) living in a communitty is given by the

Algebra ->  Rate-of-work-word-problems -> SOLUTION: hi! can u help me with these questions.? thank u! (applications of the derivative) 1) after x weeks, the number of people(or population) living in a communitty is given by the       Log On


   

Question 828243: hi! can u help me with these questions.? thank u!
(applications of the derivative)
1) after x weeks, the number of people(or population) living in a communitty is given by the function f(x)=2x^2-4x+100 provided that x is less than or equal to 1.
a.) what is the average rate of change of the population from the second week (x=2) to the fifth week (x=5)?
b.) find the rate of change of the population after the second week.
2) During a flu epidemic, medical researchers found out that the number of people infected in x days is given by the function p(x)=15x^2-x^3 for 0 less than or equal to x less than or equal to 10.
a.) find the average rate of infection for the first seven days (from day 1 to day 7).
b,) what was the rate of infection after the fourth day?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
1) after x weeks, the number of people(or population) living in a community is given by the function f%28x%29=2x%5E2-4x%2B100
After that, you typed "provided that x is less than or equal to 1".
That does not make sense I think you meant
provided that x%3E=1 , or
provided that x is greater than or equal to 1.

a.) The average rate of change of the population from the second week (x=2) to the fifth week (x=5) can be found by dividing the difference in population by the number of weeks passed.
So, in 2-5=3 weeks the population went from
f%282%29=2%2A2%5E2-4%2A2%2B100=2%2A4-8%2B100=8-8%2A100 to
f%285%29=2%2A5%5E2-4%2A5%2B100=2%2A25-20%2B100=50-20%2B100=130
The average rate of change of the population from the second week (x=2) to the fifth week (x=5) is
%28f%285%29-f%282%29%29%2F%285-2%29=%28130-100%29%2F%285-2%29=30%2F3=highlight%2810%29
That average rate is the slope of the line connecting the points for x=2 and x=3 on the graph.
graph%28300%2C300%2C-2%2C8%2C-20%2C180%2C10x%2B80%2C2x%5E2-4x%2B100%29

b.) find the rate of change of the population after the second week.
At the point x=2 (after the second week, the change of the population is given by the value of the derivative of f(x) at x=2 .
If you have been taught about derivatives, you would know that the derivative of f%28x%29 is
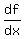
df%2Fdx%28x%29=2%2A%282x%29-4=4x-4
and for x=2 its value is
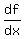
df%2Fdx%282%29=4%2A2-4=8-4=highlight%284%29
That rate at the point with x=2 is the slope of the tangent to the graph at the point with x=2 .
graph%28300%2C300%2C-2%2C8%2C-20%2C180%2C4x%2B92%2C2x%5E2-4x%2B100%29

2) During a flu epidemic, medical researchers found out that the number of people infected in x days is given by the function p%28x%29=15x%5E2-x%5E3 for 0%3C=x%3C=10 (for x between 0 and 10, inclusive) .
(Clumsier alternative wordings:
for x greater than or equal to 0, but lesser than or equal to 10,
or if you want a more unwieldy mouthful, for x such that 0 is less than or equal to x, and x is less than or equal to 10).
a.) find the average rate of infection for the first seven days (from day 1 to day 7).
As done above,
p%281%29=15%2A1%5E2-1%5E3=15-1=14 , and
p%287%29=15%2A7%5E2-7%5E3=15%2A49-343=735-343=392
%28f%287%29-f%281%29%29%2F%287-1%29=%28392-14%29%2F%287-1%29=378%2F6=highlight%2863%29
b) what was the rate of infection after the fourth day?
The derivative is
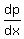
dp%2Fdx%28x%29=15%2A%282x%29-3x%5E2=30x-3x%5E2
and for x=4 its value is
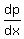
dp%2Fdx%284%29=30%2A4-3%2A4%5E2=120-3%2A16=120-48=highlight%2872%29
That rate at the point with x=4 is the slope of the tangent to the graph at the point with x=4 , with p%284%29=15%2A4%5E2-4%5E3=15%2A16-64=240-64=176.
The graphs of 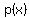p%28x%29 with one or the other line are shown below.
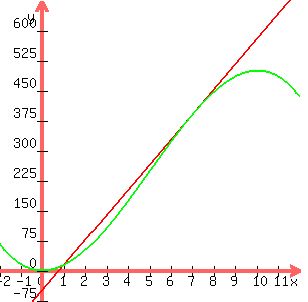
graph%28300%2C300%2C-2%2C12%2C-75%2C675%2C63x-49%2C15x%5E2-x%5E3%29
graph%28300%2C300%2C-2%2C6%2C-30%2C270%2C72x-112%2C15x%5E2-x%5E3%29 It's hard to see that the line at left is the tangent at x=4 , but a close-up does not help much either. The function is almost a straight line in the vicinity of that point.