Question 827879: In angle UTV, side UT=3, UV=4 and TV=6. In angle XYW, XY=16. The two triangles are similar such that angle X = angle U, angle Y = angle V and angle W = angle T. What is the length of XW?
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! First of all, I think you mean triangle UTV and triangle XYW. Second, since the triangles are similar, we will not need any Trigonometry to solve this.
In short, we've been given that
triangle UTV ~ triangle XWY
Similar triangles mean that, in addition to the angles being equal, the sides are proportional. This means that the ratios of pairs of corresponding sides will be equal. Since we are looking for XW, we will use a ratio that involves this side. Since X corresponds to U and T corresponds to W, the ratio of XW to its corresponding side in UTV is:
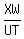
Now we to set this ratio equal to another pair of corresponding sides. It doesn't matter which pair: XY and UV or YW and TV. Since we don't know YW, I'll use XY and UT:

Substituting the known sides we get:
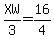
Simplifying we get:

Multiplying by 3:

P.S. Trigonometry could be used to solve this problem. But the way we did it was better:- It was faster and easier. With Trig we would have had to use the Law of Cosines (which is a somewhat complicated formula) to find angles and then use the Law of Cosines again (or maybe the Law of Sines) to find XW.
- It gives the exact answer. With Trig we would be finding decimal approximations for the angles and for XW. So we might have ended up with 12.0001 or 11.9997 or something else close to but not exactly equal to the correct answer of 12. (I just did the problem with Trig and got 12.0169!? Even if I round off less than I did, I might still never get exactly 12 for the answer!)
|
|
|