Question 827797: Show all your work and calculate the total traveling and stopping distance of a car with wooden wheels on a wooden road if a driver with a reaction time of 0.5 seconds is driving at 55 miles per hour and reading a text for 5 seconds. Give your answer in meters. Make sure to include the equations you are using and the 2 different ways to express the force of friction to calculate the acceleration due to friction. The friction constant of wood on wood is 0.4 static and 0.2 kinetic.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Conversions are in order, involving miles, hours, meters, and seconds.
The initial speed in meters per second is
 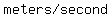
I understand that the driver keeps going at 55 miles per hour while reading a text; then realizes he/she needs to stop, but takes 0.5 second to react.
That would mean continuing to move at 55mph for 5.5 seconds.
During that time, the car will cover a distance of

If the road is horizontal and level, the normal force, pressing the car into the road is 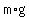 where where  is the mass of the car , and is the mass of the car , and  is the acceleration of gravity. is the acceleration of gravity.
I will use  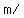 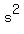 . .
If the driver, slams on the brakes so that the wheels completely stop spinning, the wheels will slide over the road and the maximum friction force that can be applied is the normal force times the kinetic friction coefficient.
So the constant friction force would be
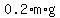 and the magnitude of the acceleration would be and the magnitude of the acceleration would be  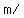  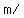 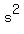 . .
We can calculate the time needed to decelerate from 24.58 m/s to 0 m/s as
  . .
That is 12.54 seconds of panic.
Then we could calculate the distance traveled while slowing down as the product of time and average velocity:
 . .
We could also calculate the distance directly as  , but I prefer to calculate it the other way. , but I prefer to calculate it the other way.
If the driver manages to brake without skidding, the wheels will not be sliding over the road, and the magnitude of the friction force can be as high as the normal force times the static friction coefficient.
So the maximum friction force would be up to
 and the magnitude of the acceleration would be up to and the magnitude of the acceleration would be up to  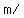  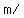 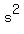 . .
If the driver manages to brake just hard enough to maintain that acceleration, the car will stop in the minimum time and distance.
We can calculate the minimum time and distance traveled while slowing down as
  and and

Depending on how skilled or panicked the driver is, the car will travel between 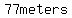 and and  after the driver satrts applying the brakes. after the driver satrts applying the brakes.
The total distance traveled, including the 5 minutes of text-reading, the reaction time, and the braking time, is between
 and and
 . .
|
|
|