We are missing how high the ball was above home plate when it was hit.
I will arbitrarily assume that the ball was hit when it was 5 feet above
the ground (home plate). This is the graph. The path of the ball is
a parabola, and it goes through (0,5) when it is hit 5 feet above the
ground. It goes through (330,16), the point the ball is at when it leaves
the park, and the point (390,0) when it hits the ground 390 feet from
home plate.
A parabola has the general equation
y = Ax²+Bx+C
Substituting in point (0,5)
5 = A(0)²+B(0)+C
5 = C
Substituting in point (330,16) and C=5
16 = A(330)²+B(330)+5
16 = 330²A+330B+5
11 = 330²A+330B
Divide through by 330
Substituting in point (390,0) and C=5
0 = A(390)²+B(390)+5
-5 = 390²A+390B
Divide through by 390
Solve the system
Subtract the 1st equation from the 2nd
Substitute in
So the equation of the parabola is
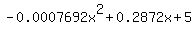To find the maximum height we use the vertex formula
The x-value of the vertex is given by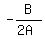 
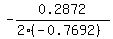= 186.7
So the ball was 186.7 feet from home plate when it reached
its maximum height.
We substitute that into
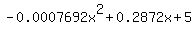
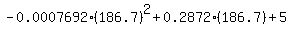
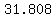The vertex of the parabola is the point (186.7,31.808).
So the maximum height of the ball was 31.808 feet and it occurred
186.7 feet from home plate.
Now this was assuming that the ball was hit at a height of 5 feet
above home plate. If you are told another height, then you'll have
to refigure it using that height. Maybe your teacher meant for you
to work it as though the ball was hit down on the ground. That would
change the answer slightly. But the principle used above is correct.
Edwin
