Question 82691: Hello Can you please help me to identify the variables, coefficients, and constants in the this algebraic expression -6x-xy+60.
Another question is Sue takes 7 minutes more to complete an illustration than
Jim. The total time taken by both of them is 6 hours. form an algebraic expression to express this and identify the variables, coefficients, and constants of the algebraic expression.
list any four situations where variables can be used to replace numbers; convert each situation into an algebraic expression. Thanks.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! identify the variables, coefficients, and constants in the this algebraic expression -6x-xy+60.
:
x & y are the variables. Different values can be assigns to x and/or y
:
-6 is the coefficient of x, it multiplies whatever x is equal to.
:
60 is the constant, 60 is always 60, on land or sea or air. It's constant
:
:
Sue takes 7 minutes more to complete an illustration than Jim. The total time
taken by both of them is 6 hours. form an algebraic expression to express this
and identify the variables, coefficients, and constants of the algebraic expression.
:
Get our time in the same units: convert 6 hr to minutes. 6*60 = 360 min
:
Let x = time required by Jim to do the job
Then (x+7) = time required by Sue to do the job
Let the completed job = 1
:
Work equation:
 + + 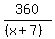 = 1 = 1
:
Get rid of those pesky denominators, mult the equation by x(x+7) and you have:
360(x+7) + 360x = x(x+7)
:
360x + 2520 + 360x = x^2 + 7x: multiplied what's in the brackets
:
720x + 2520 = x^2 + 7x: added like terms
:
0 = x^2 + 7x - 720x - 2520; put everything on the right
:
x^2 - 713x - 2520 = 0; a quadratic equation
:
The variables is x (of course), the coefficient -713, the constant is 2520
:
It doesn't tell us to solve it; but x = time (in minutes) required by Jim to do the job
:
Using my trusty Ti83 I got 713.5 min for Jim to do the job, then it would be
720.5 minutes for Sue to do it, right?
:
:
:
list any four situations where variables can be used to replace numbers; convert each situation into an algebraic expression.
:
1. Cost of a cell phone with a monthly fee of $25 and 5 cent a min:
x = number of minutes
Cost = .05x + 25
:
2. Cost to make a 1000 mi trip, tolls come to $12.50 you get 25 mi to gal,
x = gas price/gal
Cost = (1000/25)x + 12.50
:
3. Cost of rental car for one day, $25 a day and 10 cents a mile
x = miles traveled
Cost = .10x + 25
:
4. In a Democratic Fund raiser, you sell tickets for the privilege of spending
the night with Hillary.
First prize, is one night with Hillary; 2nd prize is 2 nights with Hillary.
:
Fixed cost: 3 nights in a motel = $300, each ticket cost $10.
Let x = number of tickets sold
Amount raised = 10x - 300
:
Hope you have a sense of humor.
|
|
|