Question 826703: a) Find the product of (x^2-x+1)(2x^2+3x+2)
b) Use the results of part (a) to factor 21,112 as a product of a two-digit number and a three-digit number
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 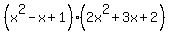
a) To multiply polynomials, you multiply each term of one polynomial by each term of the other polynomial. (In this case, with 3 terms in each polynomial, there will be 9 multiplications.) Then add like terms, if any:

Simplifying...

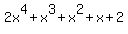
b) The "trick" for this problem is to look at the coefficients of the result from part a. The coefficients are 2, 1, 1, 1, 2. Put them all together and we have 21112 which is the number we are supposed to factor. This means that if x = 10 then 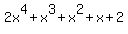 will be 21112. (If you don't see this, substitute in a 10 for the x and see how it works out.) will be 21112. (If you don't see this, substitute in a 10 for the x and see how it works out.)
Since factoring is, in effect, "un-multiplying", we already know that two factors of 21112 will be 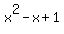 and and  with x = 10. The factor for with x = 10. The factor for 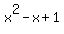 will be: will be:
 (the two-digit factor) (the two-digit factor)
And the factor for  will be: will be:
 (the three-digit factor) (the three-digit factor)
|
|
|