Question 826685: How can I algebraically find all zeros of y= (x)= 3sin(2x) + cos(x) over the interval -(pi)less than or equal to x which is less than or equal to (pi)?
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! Finding the zeros of
y = 3sin(2x) + cos(x)
means finding the solutions to:
0 = 3sin(2x) + cos(x)
Solving Trig equations like this usually starts with using algebra and/or Trig properties to transform the equation into one or more equations of the general form:
TrigFunction(expression) = number
To solve this equation we will start by using the sin(2x) = 2sin(x)cos(x) identity. Substituting for sin(2x) we get:
0 = 3(2sin(x)cos(x)) + cos(x)
which simplifies to:
0 = 6sin(x)cos(x) + cos(x)
Now we can factor out cos(x):
0 = cos(x)(6sin(x)+1)
From the Zero Product Property:
cos(x) = 0 or 6sin(x)+1 = 0
(Note how we now have two equations. This is one way to get more than one equation from a single equation.) Solving these we get:
cos(x) = 0 or sin(x) = -1/6
We now have the equations in the desired form.
Next we find the general solution.
For cos(x) = 0 we should recognize that 0 is a special angle value for cos. We should know that cos is 0 at 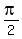 , , 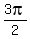 and any other angle which is co-terminal with these. So the general solution for cos(x) = 0 is: and any other angle which is co-terminal with these. So the general solution for cos(x) = 0 is:


For sin(x) = -1/6 we should recognize that 1/6 is not a special angle value for sin. So we will need our calculators. We will use 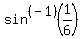 to find the reference angle. (Note: Do not use negative values when finding reference angles!) With my calculator set to radian mode, I get a reference angle, rounded to 4 places, of 0.1674. Since the 1/6 was negative (Here is where we use the fact that the sin is negative!) and since sin is negative in the 3rd and 4th quadrants we get the following general solution equations for sin(x) = -1/6: to find the reference angle. (Note: Do not use negative values when finding reference angles!) With my calculator set to radian mode, I get a reference angle, rounded to 4 places, of 0.1674. Since the 1/6 was negative (Here is where we use the fact that the sin is negative!) and since sin is negative in the 3rd and 4th quadrants we get the following general solution equations for sin(x) = -1/6:
 for the 3rd quadrant for the 3rd quadrant
 for the 4th quadrant for the 4th quadrant
Together, the general solution equations for 0 = 3sin(2x) + cos(x) are:




The general solution equations express the infinite set of solutions to the equation. Many problems, like this one, ask for solutions which are in a given interval. This time the interval is  To find these answers we replace the n's in the equations with various integers until we have found all the x's which are in the interval. To find these answers we replace the n's in the equations with various integers until we have found all the x's which are in the interval.
From  ... ...
If n = 0 then 
If n = 1 (or greater) then x is too large for the interval.
If n = -1 (or smaller) then x is too small for the interval.
From  ... ...
If n = 0 (or larger) then x is too large for the interval.
If n = -1 then 
If n = -2 or smaller then x is too small for the interval.
From  ... ...
If n = 0 (or larger) then x is too large for the interval.
If n = -1 then 
If n = -2 or smaller then x is too small for the interval.
From  ... ...
If n = 0 then 
If n = 1 (or greater) then x is too large for the interval.
If n = -1 (or smaller) then x is too small for the interval.
Altogether, the solutions to 0 = 3sin(2x) + cos(x) (and therefore the zeros of f(x) = 3sin(2x) + cos(x)) within the specified interval are:
 , ,  , ,  and and 
P.S. Feel free to replace the 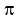 in in 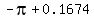 with a decimal approximation and then add the two decimals. with a decimal approximation and then add the two decimals.
|
|
|