SOLUTION: If csc theta = 2/√3, P theta is in 2 Q, then cos theta is equal to: a) -√3/2 b) √3/2 c) 3/4 d) -3/4

It's none of those answers.  I'll do it two ways to show that the
correct answer is , as the other tutor has just flatly 
stated with no explanation.  (BTW, a tutor should do more than give
answers. Too many teachers know their subject but can't teach it!).

First way:

Draw the picture of angle  in the second quadrant Q2. 
Since the cosecant is hypotenuse/opposite or r/y, and since we are given 
, make r=2 and y=, and calculate x using the 
Pythagorean theorem:

    x²+y² = r²
x²+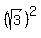 = 2²
    x²+3 = 4
      x² = 1
       x = ±√1
       x = ±1, we take x = -1 

We take x negative because it goes left from the origin, 
and we ALWAYS take r positive because it begins on the
right side of the x-axis and doesn't change its sign when
it swings around into the other quadrants. 



We want .  The cosine is adjacent/hypotenuse or x/r,
so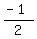 

--------------------------------

Second way, using these identities:

1.  

2.  

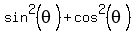Using 1.,
   
     
     
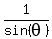
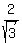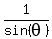Cross-multiply:
     
      

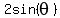
Using 2.,

    
     
         
            
            
            
               
              

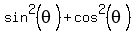
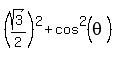
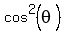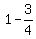
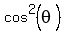
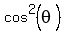
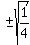
Since the cosine is negative in the second quadrant Q2,

              

Edwin