Question 825731: Find all zeros of the function f(x)=x^2(x-3)(x^3-8)
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Finding zeros of a polynomial usually involves factoring the polynomial. This function is already partially factored so some of our work has already been done.
The factor at the end, 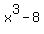 , is a difference of cubes, , is a difference of cubes, 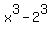 . So we can use the difference of cubes pattern, . So we can use the difference of cubes pattern,  , to factor it: , to factor it:

The last factor will not factor further. But it is a quadratic so we can use the quadratic formula to find its roots:

Simplifying...










which is short for:
 or or 
These are two of the roots of f(x).
We will get the remaining roots from the other factors:

The other roots will be the values for x that make a factor zero. For the first factor,  , we get a root of x = 0. And since x is a factor twice in , we get a root of x = 0. And since x is a factor twice in  , zero counts as a root twice! (This is called a double root.) , zero counts as a root twice! (This is called a double root.)
For the other factors we should get roots of x = 3 and x = 2.
Altogether, the roots of f(x) are: 0, 0, 2, 3, 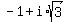 and and 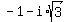
P.S. This is a polynomial, not a rational function. Please post in an appropriate category.
|
|
|