SOLUTION: Given 3+i is a root, determine all other roots of f(x)=x^4-10x^3+47x^2-118x+130. Thanks in advance!

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Given 3+i is a root, determine all other roots of f(x)=x^4-10x^3+47x^2-118x+130. Thanks in advance!      Log On


   

Question 825707: Given 3+i is a root, determine all other roots of f(x)=x^4-10x^3+47x^2-118x+130.
Thanks in advance!
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
Since f(x) is of degree 4 it will have 4 roots. We've been given one root so we have three more to find.

If a polynomial with real coefficients, like f(x), has a complex root, like f(x), then the complex conjugate of that root is also a root of the polynomial. (Standard form for complex numbers is a + bi. The complex conjugate for this is a - bi (or a + (-b)i).) So if 3 + i is a root of f(x) then so is 3 - i. Now we have two of the four roots.

To find the remaining roots we should factor f(x). This will be easier if we take advantage of the two roots we already have. When some number, let's call it "r" for root, is a root of a polynomial then (x - r) is a factor of that polynomial. So we now know that both (x - (3 + i)) [or (x - 3 - i)] and (x - (3 - i)) [or (x - 3 + i)] are factors of f(x). So:
f(x) = (x - 3 - i)(x - 3 + i)(x - ?)(x - ??)
In order to find the other factors we will divide f(x) by the two factors we have. And believe it or not, this will be easier if we multiply the two factors together and divide f(x) by the product.

To multiply (x - 3 - i)(x - 3 + i) we will use some grouping:
((x - 3) - i)((x - 3) + i)
and a clever use of the %28a%2Bb%29%28a-b%29=a%5E2-b%5E2 pattern. Using (x-3) as the "a" and "i" as the "b", the pattern tells us how the multiplication works out:
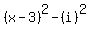
%28x-3%29%5E2-%28i%29%5E2
Now we simplify. By definition i%5E2+=+-1. And we can use another pattern, %28a-b%29%5E2+=+a%5E2-2ab%2Bb%5E2 to square (x-3) correctly:
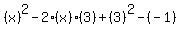
%28x%29%5E2-2%28x%29%283%29%2B%283%29%5E2-%28-1%29
Simplifying...
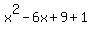
x%5E2-6x%2B9%2B1
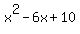
x%5E2-6x%2B10
(Notice how the i's are gone. This is why multiplying the two factors together first makes the division easier.) Now we will divide f(x) by 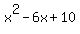x%5E2-6x%2B10 using long division:
            x^2 -  4x   +  13
           ___________________________________
x^2-6x+10 / x^4 - 10x^3 + 47x^2 - 118x + 130
            x^4 -  6x^3 + 10x^2
            --------------------
                -  4x^3 + 37x^2 - 118x
                -  4x^3 + 24x^2 -  40x
                -----------------------
                          13x^2 -  78x + 130
                          13x^2 -  78x + 130
                          ------------------
                                           0
It divided evenly (as we knew it would). So:
f%28x%29+=+%28x+-+3+-+i%29%28x+-+3+%2B+i%29%28x%5E2-4x%2B13%29
The last factor does not factor further. But it is a quadratic so we can use the quadratic formula to find its roots:
x+=+%28-%28-4%29+%2B-+sqrt%28%28-4%29%5E2-4%281%29%2813%29%29%29%2F2%281%29
Simplifying:
x+=+%284+%2B-+sqrt%2816-4%281%29%2813%29%29%29%2F2
x+=+%284+%2B-+sqrt%2816-52%29%29%2F2
x+=+%284+%2B-+sqrt%28-36%29%29%2F2
x+=+%284+%2B-+sqrt%28-1%2A36%29%29%2F2
x+=+%284+%2B-+sqrt%28-1%29%2Asqrt%2836%29%29%2F2
x+=+%284+%2B-+i%2A6%29%2F2
x+=+%284+%2B-+6i%29%2F2
x+=+%282%282+%2B-+3i%29%29%2F2
x+=+%28cross%282%29%282+%2B-+3i%29%29%2Fcross%282%29
x+=+2+%2B-+3i
which is short for:
x+=+2+%2B+3i or x+=+2+-+3i

This makes the 4 roots of f(x): 3 + i, 3 - i, 2 + 3i and 2 - 3i

P.S. If you really dislike long division of polynomials and if you're not afraid to work with i's, you could have divided f(x) by (x - (3 + i)) and (x - (3 - i)) individually using synthetic division. First we'll divide by (x - (3 + i)):
3+i  |   1   -10     47     -118      130
------         3+i  -22-4i    79+13i -130
        -----------------------------------
         1    -7+i   25-4i   -39+13i    0
Next, we'll divide the result by (x - (3 - i)):
3-i  |   1    -7+i   25-4i   -39+13i
------         3-i  -12+4i    39-13i
        ----------------------------
         1    -4     13       0
leaving the factor of 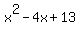x%5E2-4x%2B13 that we found earlier using long division.