|
Question 825613: If x=3 is the equation of the axis of symmetry of the graph of y=x^2-6x+10 what is the y coordinate of the turning point ?
Found 3 solutions by phoihe001, Edwin McCravy, Fermat:
Answer by phoihe001(34)   (Show Source):
Answer by Edwin McCravy(20065)  (Show Source):
You can put this solution on YOUR website!
The above "tutor" should not be on here.
Here is the graph of y=x²-6x+10 and the green line through x=3
is its axis of symmetry:
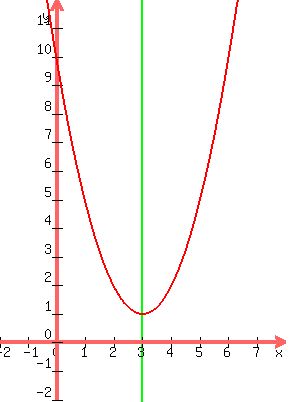So its turning point is found when we substitute 3 for x in
y = x²-6x+10
y = 3²-6(3)+10
y = 9-18+10
y = -9+10
y = 1
So the turning point is where the green line x=3 crosses the
parabola graph. It's x-coordinate is 3 and its y-coordinate
is 1.
So the turning point is (3,1)
You were just asked for the y-coordinate, so it's 1.
Edwin
Answer by Fermat(136)  (Show Source):
You can put this solution on YOUR website! A standard quadratic equation like y = x^2 is a U-shaped curve that is centred on the origin, has its axis of symmetry as the line x = 0, and has its turning point at the origin also, i.e. where y = 0.
If we translate this graph about the x-y plane such that its origin is now at the coords (h,k), then the new equation of the curve is,
(y-k) = (x-h)^2
And here the axis of symmetry is the line x = h and the bottom of the curve (its turning point) is on the line y = k.
Our graph is y = x^2 - 6x + 10
completing the square on the rhs gives us,
y = x^2 - 6x + 9 + 1
y = (x - 3)^2 + 1
(y - 1) = (x - 3)^2
Here (h,k) = (3,1).
So the origin of this curve is the point (x,y) = (3,1).
Thus the y-coordinate of its turning point is y = 1.
|
|
|
| |
