|
Question 825489: find the domain of (fog)x given that f(x) =1/2-x and g(x) =2/x.
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'm guessing that is not what you posted:

but

because it makes the problem more interesting. If I am wrong, then I hope you will be able to figure out the answer to the real problem from the solution I show you below. If I am right, then please put parentheses around numerators and denominators which are not just a positive number or variable. For example:
f(x) = 1/(2-x)
(fog)(x) means f(g(x)). And f(g(x)) represents the output of f when g(x) is used as input. So:
(fog)(x) = 
The domain of (fog)(x) is the set of all the possible values of x which can be used. Often the domain is all real numbers. But in this case, with an x in the denominator of 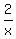 and in the denominator of and in the denominator of 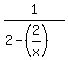 , we have to make sure that neither denominator becomes a zero, which we can never allow to happen!. So let's see what values of x would make each denominator equal to zero: , we have to make sure that neither denominator becomes a zero, which we can never allow to happen!. So let's see what values of x would make each denominator equal to zero:
For 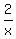 , the denominator would be zero only if x was zero, too. For , the denominator would be zero only if x was zero, too. For 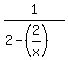 , the denominator would be zero only if x was 1. (If you cannot see this, then set the denominator equal to zero: , the denominator would be zero only if x was 1. (If you cannot see this, then set the denominator equal to zero:

and solve for x. You should get x = 1.
Remember, we have found what numbers x cannot be. The domain is the set of numbers x can be. So the domain for (fog)(x) is: All real numbers except 0 and 1.
|
|
|
| |