SOLUTION: I am solving a 7th grade math text book, and I came across this one: a^x = b^y = c^z, and a³ = b²c, then (3/x) - (2/y) = ? I tried: --> c = (a³/b²) --> a = cube root(b²c)

Algebra ->  Exponents -> SOLUTION: I am solving a 7th grade math text book, and I came across this one: a^x = b^y = c^z, and a³ = b²c, then (3/x) - (2/y) = ? I tried: --> c = (a³/b²) --> a = cube root(b²c)       Log On


   

Question 825465: I am solving a 7th grade math text book, and I came across this one:
a^x = b^y = c^z, and a³ = b²c, then (3/x) - (2/y) = ?
I tried:
--> c = (a³/b²)
--> a = cube root(b²c)
--> b = √(a³/c),
but couldn't arrive at a conclusion; and also thought there should be a simpler way of solving this.
Please help.
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
If this really came out of a 7th grade book, then there must be a much simpler way to solve this than the one I am about to show you. I just can't see anything simpler than what you are about to see. If you believe that there is a simpler solution, then please re-post your question and specify "without using logarithms" so you don't get a solution like below.

As I figured out this solution, my thought process was...
  • To find (3/x) - (2/y) we will need to find an expression for 3/x and for 2/y
  • To find expressions for 3/x and 2/y we will need an expression for x and for y. (A simpler expression, if one exists, probably does not make this assumption.)
  • To find expressions for x and for y we will need to use logarithms since the only place we can find them at the start is in exponents (and logarithms are a tool which can be used to solve for an exponent). (Logarithms are almost never taught in 7th grade. This is why I assume there must be a different, simpler solution.)
To start, I will introduce another, temporary variable (which we'll name "q") and say the q is also equal to all those powers of a, b and c:
q+=+a%5Ex+=+b%5Ey+=+c%5Ez
Now we will solve for x, y and z. First we will use
q+=+a%5Ex
to solve for x. Finding the log of each side:
log%28%28q%29%29+=+log%28%28a%5Ex%29%29
Next we use a property of logarithms, log%28m%2C+%28p%5En%29%29+=+n%2Alog%28m%2C+%28p%29%29, to "move" the exponent out in front:
log%28%28q%29%29+=+x%2Alog%28%28a%29%29
Dividing both sides by log(a):
log%28%28q%29%29%2Flog%28%28a%29%29+=+x
Now we will find an expression for 3/x. Taking the reciprocal of each side:
log%28%28a%29%29%2Flog%28%28q%29%29+=+1%2Fx
Multiplying each side by 3:
3log%28%28a%29%29%2Flog%28%28q%29%29+=+3%2Fx

Now we will use
q+=+b%5Ey to get an expression for y first, then an expression for 2/y. The steps are similar to the ones we used above so I will not explain them again:
q+=+b%5Ey
log%28%28q%29%29+=+log%28%28b%5Ey%29%29
log%28%28q%29%29+=+y%2Alog%28%28b%29%29
log%28%28q%29%29%2Flog%28%28b%29%29+=+y
log%28%28b%29%29%2Flog%28%28q%29%29+=+1%2Fy
2log%28%28b%29%29%2Flog%28%28q%29%29+=+2%2Fy

Now we will use q+=+c%5Ez to get an expression for z:
q+=+c%5Ez
log%28%28q%29%29+=+log%28%28c%5Ez%29%29
log%28%28q%29%29+=+z%2Alog%28%28c%29%29
log%28%28q%29%29%2Flog%28%28c%29%29+=+z

Now let's look at what we have for 3/x - 2/y. Substituting in the expressions we found above we should get:
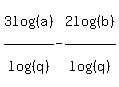
3log%28%28a%29%29%2Flog%28%28q%29%29+-+2log%28%28b%29%29%2Flog%28%28q%29%29
These already have the same denominator so we can subtract:
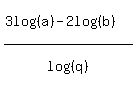
%283log%28%28a%29%29-+2log%28%28b%29%29%29%2Flog%28%28q%29%29+
Not very interesting yet. But if we use that property for logarithms, in the other direction, we can move the coefficients of the logs into the arguments:
%28log%28%28a%5E3%29%29-+log%28%28b%5E2%29%29%29%2Flog%28%28q%29%29+
Still not very interesting. But if we use another property of logarithms, log%28m%2C+%28p%29%29+-+log%28m%2C+%28v%29%29+=+log%28m%2C+%28p%2Fv%29%29, to combine these logs:
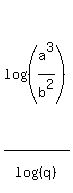
log%28%28a%5E3%2Fb%5E2%29%29%2Flog%28%28q%29%29+
Starting to look interesting... From a%5E3+=+b%5E2+%2Ac, we can get a%5E3%2Fb%5E2+=+c. Substituting this in we get:
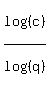
log%28%28c%29%29%2Flog%28%28q%29%29+
This looks vaguely familiar. Looking back we can see that
log%28%28q%29%29%2Flog%28%28c%29%29+=+z
The left side of this is the reciprocal of what we currently have for 3/x - 2/y! So:
3%2Fx-2%2Fy=1%2Fz

P.S. If you find a simpler, logarithm-less solution to this, please tell me what it is via a "thank you" for this solution.