SOLUTION: List the possible rational zeros of the function using the rational zeros theorem. g(x) = {{{ x^5-4x^3+2x+12}}}

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: List the possible rational zeros of the function using the rational zeros theorem. g(x) = {{{ x^5-4x^3+2x+12}}}      Log On


   

Question 825415: List the possible rational zeros of the function using the rational zeros theorem.
g(x) = 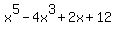+x%5E5-4x%5E3%2B2x%2B12
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
The possible rational zeros of a polynomial are all the ratios, positive and negative, that can be formed using factors of the constant term (at the end) in the numerator and factors of the leading coefficient (at the beginning) in the denominator.

With a constant term of 12 and a leading coefficient of 1, g(x) has the following list of possible rational zeros:
+1/1, +2/1, +3/1, +4/1, +6/1 and +12/1
which simplifies to:
+1, +2, +3, +4, +6 and +12