Question 825413: Find all the real zeros of the function.
h(x)= 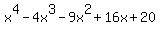
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! To find the zeros of h(x) we need to factor it. And of the factoring methods, I can only see that factoring by trial and error of the possible rational roots/zeros could work (to start).
The possible rational roots/zeros of a polynomial are all the ratios, positive and negative, which can be formed using a factor of the constant term (at the end) in the numerator and a factor of the leading coefficient (at the beginning) in the denominator. With h(x)'s constant term of 20 and leading coefficient of 1 we get the following list of possible rational roots/zeros for h(x):
+1/1, +2/1, +4/1, +5/1, +10/1 and +20/1
which reduce to:
+1, +2, +4, +5, +10 and +20
Now we can try these to see if any of them are actual root/zero. We can try 1 mentally since powers of 1 are extremely easy. We shoujld find that h(1) is not zero. So 1 is not a root/zero. Now we'll try 2. For this we will use synthetic division:
2 | 1 -4 -9 16 20
---- 2 -4 -26 -20
-----------------------
1 -2 -13 -10 0
And we have a winner! The zero in the lower right corner is the remainder. And if the remainder is zero then the division divided evenly. And what we divided by was (x-2) so 2 is a root/zero of h(x)! Not only that but the rest of the bottom row is the quotient/other factor. The "1 -2 -13 -10" translate into 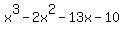 . So now: . So now:

As we look for more roots/zeros, we only need to factor the second factor above. (This means that +20 are no longer possible roots/zeros.) Let's try 2 again. (Roots/zeros can be roots/zeros multiple times!)
2 | 1 -2 -13 -10
---- 2 0 -26
---------------------
1 0 -13 -36
No. If we try 4, it doesn't work either. But 5...
5 | 1 -2 -13 -10
---- 5 15 10
---------------------
1 3 2 0
And we have a second root/zero. Now:

Now we factor 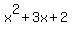 . This is a quadratic (so we no longer have to use the trial and error method). It factors easily. So: . This is a quadratic (so we no longer have to use the trial and error method). It factors easily. So:

This makes the roots/zeros of h(x): 2, 5, -1 and -2.
P.S. Please post your problems in an appropriate category. "test" should be used only if there is no relevant, established category. This problem should be the the "Polynomials" category.
Problems posted in relevant categories get quicker responses!
|
|
|