SOLUTION: Identify the vertical asymptotes for each equation State the domain for each equation. {{{y= (x^2+7x+12)/(x^2-4)}}} {{{y= (x^3-5x^2-14x)/(x^2+2x+1)}}}

Hi, there--

PROBLEM:
Identify the vertical asymptotes for each equation. State the domain.
a) 

b) 

SOLUTION:
Consider the first equation:


We typically have restrictions on the domain of a function for two reasons: taking the square 
root of a negative number, and division by zero. There are no square roots in this equation, 
but we are dividing by a polynomial. We need to find any value of x for which the denominator 
will equal 0 to avoid division by zero (a big no-no!)


Find the zeroes (roots) for the polynomial in the denominator. Set the denominator equal to 
zero and solve for x.



 or 

In order to avoid division by zero, we restrict our domain to all the real numbers except -2 
and 2. 

Domain: all the real numbers, such that 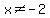 or 

In bracket notation (using a "sideways 8" for infinity):
Domain: (-infinity,-2) U (-2,2) U (2, infinity)


Vertical asymptotes are vertical lines which correspond to the zeroes of the denominator of a 
rational function. We have already found the zeros for the denominator of this function:

Vertical Asymptotes:  and 

I will leave the second equation for you to work out on your own. Feel free to email me at the 
address below if you get stuck or want to check your answers.

Good luck!
Mrs. Figgy
math.in.the.vortex@gmail.com