SOLUTION: In a regular polygon, the ratio of the measure of an exterior angle to the measure of an interior angle is 2:13. How many sides does the polygon have? Thanks in advance.

Click here to see ALL problems on Polygons

Question 825165: In a regular polygon, the ratio of the measure of an exterior angle to the measure of an interior angle is 2:13. How many sides does the polygon have?
Thanks in advance.
Found 2 solutions by jsmallt9, KMST:
Answer by jsmallt9(3758) (Show Source):
You can put this solution on YOUR website!
An exterior and and interior angle of a polygon form a linear pair. This makes them are supplementary. So if
x = the smaller angle, then
180 - x = the larger angle

Then, since the ratio of these is 2:13:

This can be solved. Cross-multiplying we get:

Simplifying:

Adding 2x:

Dividing by 15:

This is the exterior angle. Since the exterior angles add up to 360 and since they are all the same in a regular polygon, the number of exterior angles is:
360/24 = 15.
So the polygon has 15 exterior angles. And since the number of sides is the same as the number of exterior angles, the polygon has 15 sides, a 15-gon.

Answer by KMST(5328) (Show Source):
You can put this solution on YOUR website!
ANOTHER WAY:
In a polygon with sides,
the sum of the measures of the exterior angles is ,
and the sum of the interior angles is .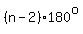
If the polygon is a regular polygon, all the exterior angles have the same measure, , and all the interior angles have the same measure .
So, for a regular polygon with sides,
, and .
The ratio is
.
Simplifying, we get
.
For the polygon of the problem, ,
so

OR MAYBE:
:::
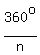