Question 825018: find the exact values of sin(A+B), cos(A+B), and tan(A+B), given:
a.) sin A = 8/17, tan B = 5/12, A and B in Q1
b.) cos A = -12/13, cot B= 24/7, A in Q2, B in Q3
c.) sin A = 1/3, sin B = 2/5, A in Q1, B in Q2
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website! find the exact values of sin(A+B), cos(A+B), and tan(A+B), given:
a.) sin A = 8/17, tan B = 5/12, A and B in Q1
Draw the picture of angle A in the first quadrant Q1, and since
the sine is opposite/hypotenuse or y/r, and since we are given
sin A = 8/17, make y=8 and r=17, and calculate x using the
Pythagorean theorem:
x²+y² = r²
x²+8² = 17²
x²+64 = 289
x² = 225
x = √225
x = 15
 Draw the picture of angle B in the first quadrant Q1, and since
the tangent is opposite/adjacent or y/x, and since we are given
tan B = 5/12, make y=5 and x=12, and calculate r using the
Pythagorean theorem:
x²+y² = r²
12²+5² = r²
144+25 = r²
169 = r²
√169 = r
13 = r
Draw the picture of angle B in the first quadrant Q1, and since
the tangent is opposite/adjacent or y/x, and since we are given
tan B = 5/12, make y=5 and x=12, and calculate r using the
Pythagorean theorem:
x²+y² = r²
12²+5² = r²
144+25 = r²
169 = r²
√169 = r
13 = r
 Now we can solve the problem using the above graphs,
with sine = y/r, cosine = x/r and tangent = y/x, and
the identities:
sin(A+B) = sin(A)cos(B)+cos(A)sin(B)
sin(A+B) =
Now we can solve the problem using the above graphs,
with sine = y/r, cosine = x/r and tangent = y/x, and
the identities:
sin(A+B) = sin(A)cos(B)+cos(A)sin(B)
sin(A+B) = 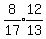  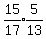 sin(A+B) =
sin(A+B) = 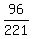  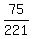 sin(A+B) =
sin(A+B) = 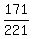 cos(A+B) = cos(A)cos(B)-sin(A)sin(B)
cos(A+B) =
cos(A+B) = cos(A)cos(B)-sin(A)sin(B)
cos(A+B) = 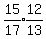  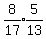 cos(A+B) =
cos(A+B) = 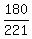  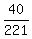 cos(A+B) =
cos(A+B) = 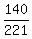 tan(A+B) =
tan(A+B) =  = =  = = 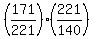 = = 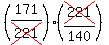 = = 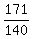 ---------------------------------------------------
b.) cos A = -12/13, cot B= 24/7, A in Q2, B in Q3
Draw the picture of angle A in the second quadrant Q2, and since
the cosine is adjacent/hypotenuse or x/r, and since we are given
cos A = -12/13, make x=-12 and r=13, and calculate y using the
Pythagorean theorem:
x²+y² = r²
(-12)²+y² = 13²
144+y² = 169
y² = 25
y = √25 = r
y = 5
We take y positive because it goes up from the x-axis,
and we take x negative because it goes to the left of
the origin on the x-axis:
---------------------------------------------------
b.) cos A = -12/13, cot B= 24/7, A in Q2, B in Q3
Draw the picture of angle A in the second quadrant Q2, and since
the cosine is adjacent/hypotenuse or x/r, and since we are given
cos A = -12/13, make x=-12 and r=13, and calculate y using the
Pythagorean theorem:
x²+y² = r²
(-12)²+y² = 13²
144+y² = 169
y² = 25
y = √25 = r
y = 5
We take y positive because it goes up from the x-axis,
and we take x negative because it goes to the left of
the origin on the x-axis:
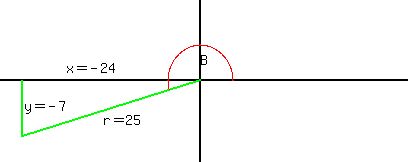
 Draw the picture of angle B in the third quadrant Q3, and since
the cotangent is adjacent/opposite or x/y, and since we are given
cot B = 24/7, make x=-24 and y=-7, and calculate r using the
Pythagorean theorem. We take y negative because it goes down,
and we take x negative because it goes left.
x²+y² = r²
(-7)²+(-24)² = r²
49+576 = r²
625 = r²
√625 = r
(r is always taken positive)
Draw the picture of angle B in the third quadrant Q3, and since
the cotangent is adjacent/opposite or x/y, and since we are given
cot B = 24/7, make x=-24 and y=-7, and calculate r using the
Pythagorean theorem. We take y negative because it goes down,
and we take x negative because it goes left.
x²+y² = r²
(-7)²+(-24)² = r²
49+576 = r²
625 = r²
√625 = r
(r is always taken positive)
 Now we can solve the problem using the above graphs,
with sine = y/r, cosine = x/r and tangent = y/x, and
the identities:
sin(A+B) = sin(A)cos(B)+cos(A)sin(B)
sin(A+B) =
Now we can solve the problem using the above graphs,
with sine = y/r, cosine = x/r and tangent = y/x, and
the identities:
sin(A+B) = sin(A)cos(B)+cos(A)sin(B)
sin(A+B) = 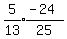  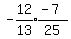 sin(A+B) =
sin(A+B) = 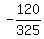  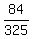 sin(A+B) =
sin(A+B) = 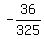 cos(A+B) = cos(A)cos(B)-sin(A)sin(B)
cos(A+B) =
cos(A+B) = cos(A)cos(B)-sin(A)sin(B)
cos(A+B) = 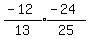  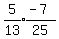 cos(A+B) =
cos(A+B) = 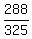  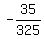 cos(A+B) =
cos(A+B) = 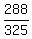  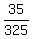 cos(A+B) =
cos(A+B) = 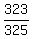 tan(A+B) =
tan(A+B) =  = =  = = 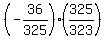 = = 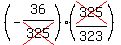 = = 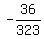 ---------------------------------------------------
c.) sin A = 1/3, sin B = 2/5, A in Q1, B in Q2
You can do that one yourself. Draw the angles in
the correct quadrants. Use the Pythagorean
theorem to get the third sides. You will do it the
same way as the other two except the x's will have
to be left as square roots instead of whole numbers,
as the first two came out to be. For angle A, x will
be √8 = √4·2 = 2√2. For angle B, x will be -√21.
Edwin
---------------------------------------------------
c.) sin A = 1/3, sin B = 2/5, A in Q1, B in Q2
You can do that one yourself. Draw the angles in
the correct quadrants. Use the Pythagorean
theorem to get the third sides. You will do it the
same way as the other two except the x's will have
to be left as square roots instead of whole numbers,
as the first two came out to be. For angle A, x will
be √8 = √4·2 = 2√2. For angle B, x will be -√21.
Edwin
|
|
|