Question 824931: Rain falls on a cubic block of solid wood (with sides of length 16 in each direction) that is left outside, soaking the five out of the six faces that are exposed to the rain. If this block is cut into 2-inch cubes, what proportion of these cubes will have more than one wet face?
Please help me on this question. I wasn't sure what type of question this was, so I put it as miscellaneous. Thank you!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Once the block is cut into smaller cubes with 2-inch sides,
but before those cubes get separated,
the original cube looks like this:
 It has been cut into It has been cut into  smaller cubes. smaller cubes.
Each face of the original cube looks like this:
 . .
On each face of the original cube there are  small cubes, in the middle, that can only get wet on one face. The other cubes around the edges could get wet on more than one face. The edges of each face include small cubes, in the middle, that can only get wet on one face. The other cubes around the edges could get wet on more than one face. The edges of each face include 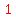 small cube at each corner, and an additional small cube at each corner, and an additional  cubes, in the middle of each edge, that are not at the corners. cubes, in the middle of each edge, that are not at the corners.
Parts of the original cube are wet from the rain.
What parts? How many faces, edges, and corners?
Of the 6 faces of the original large cube,  are wet. are wet.
Each of the  corners of the original large cube is wet on at least 2 of the 3 faces that make up that corner. corners of the original large cube is wet on at least 2 of the 3 faces that make up that corner.
Of the 12 edges, of the original large cube, the 4 edges at the bottom are not wet wet on the bottom side, while the remaining  edges are wet on both sides. edges are wet on both sides.
What small cubes are wet on more than one face?
The  cubes at the corners and another cubes at the corners and another  cubes on each of the cubes on each of the  edges wet on both sides. edges wet on both sides.
Those add up to
 . .
Those small cubes wet on more than one face are  of the of the  small cubes. small cubes.
As a fraction/ratio, that is 
|
|
|