Question 824722: Please help me with these questions :
1) The equations ax^2 +bx+c =0 and bx^2 +ax+c=0 have the same roots. Show that a+b+c=0 where a is not =b and c is not =0.
2) show that the equation (x-k)^ 2 +2x-k has real roots and hence show that 1
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1) If the equations  and and  , ,
where 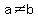 and and 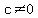 , have a common root, that root will satisfy , have a common root, that root will satisfy
 . .
Solving:





If  were a solution of were a solution of  , ,  would be zero: would be zero:
 . .
So we know that,
 --> --> 



We can divide both sides of the equal sign by 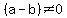 , to get , to get
 . .
(We know that 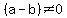 because because 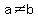 ). ).
Since we have concluded that only  could be a solution to both equations, could be a solution to both equations,
substituting  for for  must make both equations true. must make both equations true.
Substituting into  , ,
we get



We get the same using the other equation.
The two equations could be  , with roots , with roots  and and  , ,
and  , with roots , with roots  and and  . .
NOTE:
The only solution that we found that could be a common solution to both equations was  . .
There must be two more, different solutions, one for each equation.
It cannot be  as a double solution to both equations, as a double solution to both equations,
because that would require  . .
If  were the only solution to both equations, the equations would be were the only solution to both equations, the equations would be
 , and , and
 . .
The independent term in both should be
 and and  . .
That would require  . .
2) 





So  --> -->  <--> <--> 
Alternatively,



For real solutions we need the discriminant to be non negative




 <--> <--> 
|
|
|