SOLUTION: A point P moves such that it is always twice as far from the points (4,0) as it is on the line x = 1 a) find the equation of the locus b) identify the locus and graph Thanks

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: A point P moves such that it is always twice as far from the points (4,0) as it is on the line x = 1 a) find the equation of the locus b) identify the locus and graph Thanks       Log On


   

Question 824635: A point P moves such that it is always twice as far from the points (4,0) as it is on the line x = 1
a) find the equation of the locus
b) identify the locus and graph
Thanks very much:)
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
Let point P be (x, y).
Then the distance from P to (4, 0), using the distance formula, is:
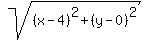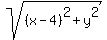
sqrt%28%28x-4%29%5E2%2B%28y-0%29%5E2%29 or just sqrt%28%28x-4%29%5E2%2By%5E2%29
Since...
  • x = 1 is a vertical line; and
  • since distance from a point to a line is measured perpendicularly; and
  • since perpendicular to vertical is horizontal
.. the distance from point P to the line x = 1 is a horizontal distance. And horizontal distances are calculated by subtracting the x-coordinates.
So the displace from point P to the line x = 1 is: 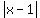abs%28x-1%29
(Note: Absolute value is used because distance should be positive. And without the absolute value x-1 would be negative if x < 1.)

We are now ready to translate "A point P moves such that it is always twice as far from the points (4,0) as it is on the line x = 1" into an equation. The translation might be easier to see if we reword the quoted sentence to: "The distance from point P to the point (4, 0) is twice as much as the distance from point P to the line x = 1."
sqrt%28%28x-4%29%5E2%2By%5E2%29+=+2%2Aabs%28x-1%29
Now we simplify. Squaring the left side should be simple. And squaring the right side is not hard, either, since x-1, after we square it, could not be negative. So the absolute value is no longer needed!
%28sqrt%28%28x-4%29%5E2%2By%5E2%29%29%5E2+=+%282%2Aabs%28x-1%29%29%5E2
%28x-4%29%5E2%2By%5E2+=+2%5E2%2A%28abs%28x-1%29%29%5E2
x%5E2-8x%2B16%2By%5E2+=+4%2A%28x-1%29%5E2
x%5E2-8x%2B16%2By%5E2+=+4%2A%28x%5E2-2x%2B1%29
x%5E2-8x%2B16%2By%5E2+=+4x%5E2-8x%2B4
Now we put the equation in standard form (for conic sections). Subtracting the entire left side from both sides we get:
0+=+3x%5E2-y%5E2-12
This is the equation for part a.

Looking at our equation, with no xy terms and with the x and y squared terms having opposite signs, we should recognize that it is the equation for a hyperbola.

To graph this hyperbola it will help to put it into the %28x-h%29%5E2%2Fa%5E2-%28y-k%29%5E2%2Fb%5E2+=+1 form for hyperbolas. Adding 12 to each side we get:
12+=+3x%5E2-y%5E2
Dividing both sides by 16 (in order to turn it into a 1):
1+=+3x%5E2%2F12-y%5E2%2F12
Reducing the the first fraction:
1+=+x%5E2%2F4-y%5E2%2F16
Rewriting the numerators to fit the form:
1+=+%28x-0%29%5E2%2F4-%28y-0%29%5E2%2F16

We can now "read" the key data:
  • With the x squared in front of the subtraction, this hyperbola has a horizontal transverse axis.
  • The "h" and "k" are zeros. So the center of the hyperbola is (0, 0) (aka the origin).
  • a%5E2+=+4. This makes a+=+2 Since "a" is the distance from the center to the vertices on the transverse axis and since center is (0, 0), the vertices are (2, 0) and (-2, 0).
  • b%5E2+=+16 so b = 4.
  • With a = 2 and b = 4, the slopes of the asymptotes are: +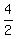4%2F2 = +2
I'll leave the graphing up to you. Here's what it should look like:
graph%28400%2C+400%2C+-8%2C+8%2C+-8%2C+8%2C+sqrt%283x%5E2-12%29%2C+-sqrt%283x%5E2-12%29%29
(Don't mind the different colors or the gaps (which are there only because algebra.com's graphing software doesn't handle nearly vertical parts of a graph well.)