Question 824528: Junior drove his rig on Interstate 10 from San Antonio and El Paso. At the halfway point he noticed that he had been averaging 80 mph, while his company requires his average speed to be 60 mph. What must be speed for the last half of the trip so that he will average 60 mph for the entire trip. Distance doesn't matter.
Found 2 solutions by TimothyLamb, MathTherapy:
Answer by TimothyLamb(4379)   (Show Source): (Show Source):
You can put this solution on YOUR website! ---
s = d / t
t = d / s
D = half trip distance
---
first half (a):
t = d / s
ta = D/80
---
second half (b):
t = d / s
tb = D/x
where x is the unknown speed for the second half
---
whole trip:
s = d / t
60 = 2D / (ta + tb)
60 = 2D / (D/80 + D/x)
60(D/80 + D/x) = 2D
60(xD/80x + 80D/80x) = 2D
(60D/80x)(x + 80) = 2D
(60/80x)(x + 80) = 2
x + 80 = 2*(80/60)x
x + 80 = (2.666666)x
(2.666666)x - x = 80
(1.666666)x = 80
x = 80/1.666666
x = 48.0
---
answer:
the speed for the last half of the trip must be: 48 mph
---
Solve and graph linear equations:
https://sooeet.com/math/linear-equation-solver.php
---
Solve quadratic equations, quadratic formula:
https://sooeet.com/math/quadratic-formula-solver.php
---
Solve systems of linear equations up to 6-equations 6-variables:
https://sooeet.com/math/system-of-linear-equations-solver.php
Answer by MathTherapy(10551)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Junior drove his rig on Interstate 10 from San Antonio and El Paso. At the halfway point he noticed that he had been averaging 80 mph, while his company requires his average speed to be 60 mph. What must be speed for the last half of the trip so that he will average 60 mph for the entire trip. Distance doesn't matter.
Let distance be D, and speed on last ˝ of trip, S
Then time he took to travel 1st ˝ of the distance = ˝D/80, or 
Time 2nd ˝ of trip should take = ˝D/S, or 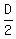 ÷ S, or ÷ S, or 
Average speed = 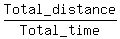
Therefore, 60 = D ÷ 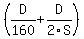
60 = D ÷  ____ ____ = =  * * 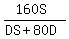


60(DS + 80D) = 160DS ------ Cross-multiplying
60DS + 4,800D = 160DS
D(60S + 4,800) = D(160S) ------ Factoring out GCF, D
60S + 4,800 = 160S
60S – 160S = - 4,800
– 100S = - 4,800
S, or speed on 2nd ˝ of journey should be: 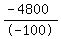 , or , or  mph mph
You can do the check!!
Send comments, “thank-yous,” and inquiries to “D” at MathMadEzy@aol.com.
Further help is available, online or in-person,for a fee, obviously.
For FREE info and answers to questions about the ASVAB exam, the NYS 3 – 8 city/state wide exams,
GENERAL MATH QUESTIONS, MATH HOMEWORK QUESTIONS, or MATH QUESTIONS related to the Regents Integrated Algebra,
Regents Geometry, Regents Algebra 2/Trigonometry, SHSAT, COOP/HSPT/TACHS, PSAT, SAT, ACT, SSAT/ISEE, GRE, CLEP,
and the GED, you can visit: http://asvabstudyzone.freeforums.net/.
|
|
|