Question 824514: How can KEY FEATURES be used to create any polynomial function?
What are the key features and how are they used?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I had to search online for the meaning of "key features".
That was not a phrase used when and where I learned math.
I concluded that "key features" of the graph of a polynomial include zeros, and "turning points". The list could include "end behavior" and type of symmetry", but there seems to be no widely agreed upon definition of "key features".
If a polynomial  can be factored, it can be written as can be factored, it can be written as
 , ,
Where  , ,  , ,  , and so on are the zeros of the polynomial, , and so on are the zeros of the polynomial,
and 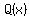 is a polynomial of even degree that cannot be factored (without zeros), is a polynomial of even degree that cannot be factored (without zeros),
such as 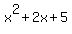 , or a "polynomial" of degree zero (a constant), , or a "polynomial" of degree zero (a constant),
such as  or or  . .
Needles to say, a polynomial of degree  can have at most can have at most  zeros. zeros.
Key features are used to graph a polynomial.
They are also used to try to figure out the function when given the graph, or some limited information about the graph.
ZEROS:
One use of zeros, is to get information about the degree of a polynomial.
A polynomial with no zeros, or an even number of zeros must have have an even degree.
A polynomial with an odd number of zeros must have an odd degree.
A polynomial with  zeros has zeros has  . .
TURNING POINTS:
A polynomial of degree  (a linear function) graphs as a straight line and has (a linear function) graphs as a straight line and has  turning points. turning points.
A polynomial of degree  (a quadratic function) graphs as a parabola and has (a quadratic function) graphs as a parabola and has  turning point (the vertex). turning point (the vertex).
A polynomial of degree  has at most has at most 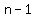 turning points. turning points.
END BEHAVIOR:
As the zero-related factors in the factored form,
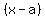 , , 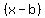 , and so on, , and so on,
change from positive to negative at  , ,  , and so on, , and so on,
outside of the interval containing all the zeros,
the polynomial will be either positive or negative,
and must continuously increase in absolute value as 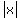 increases, increases,
because the absolute value of all the factors will be increasing.
Outside of the interval containing all the zeros,
for very large 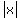 , ,
the absolute value of a polynomial function increases without bounds.
Even degree polynomials go in the same direction at both ends.
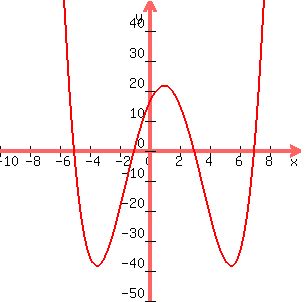 
Odd degree polynomials head in opposite directions at the ends:
 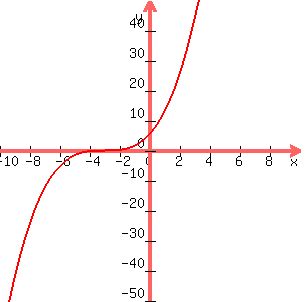
SYMMETRY:
Even degree polynomials may have graphs with line symmetry,
such as parabolas, which have an axis of symmetry.
Odd degree functions, that have opposite end behavior at both ends,
cannot have lyne symmetry, but may have point symmetry,
as seen in the graph of  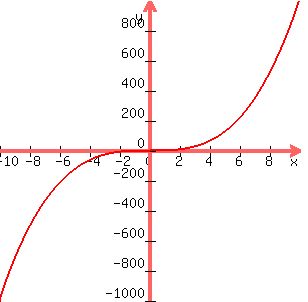 , ,
which rotated  around the origin turns into the same graph. around the origin turns into the same graph.
|
|
|