SOLUTION: Pipe A takes 16 min to fill a tank. Pipes B and C, whose cross-sectional circumferences are in the ratio 2:3, fill another tank twice as big as the first. If A has a cross-sectiona

Algebra ->  Rate-of-work-word-problems -> SOLUTION: Pipe A takes 16 min to fill a tank. Pipes B and C, whose cross-sectional circumferences are in the ratio 2:3, fill another tank twice as big as the first. If A has a cross-sectiona      Log On


   

Question 824377: Pipe A takes 16 min to fill a tank. Pipes B and C, whose cross-sectional circumferences are in the ratio 2:3, fill another tank twice as big as the first. If A has a cross-sectional circumference that is one-third of C, how long will it take for B and C to fill the second tank? (Assume the rate at which water flows through a unit cross-sectional area is same for all the three pipes.)
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
Pipe A takes 16 min to fill a tank. 
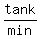
So pipe A's filling rate is 1 tank per 16 min or %281_tank%29%2F%2816_min%29 or 1%2F16tank%2Fmin
A has a cross-sectional circumference that is one-third of C
Therefore C's cross-sectional circumference is 3 times A's cross-sectional
circumference, and since area varies as the square of the circumference,
C's cross-sectional area is 3² or 9 times A's cross-sectional area. 

Since
the rate at which water flows through a unit cross-sectional area is same for all the three pipes
 therefore:

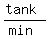
Pipe C's filling rate is 9 times A's filling rate or 9%2F16%28tank%29%2F%28min%29
Pipes B and C's cross-sectional circumferences (are) in the ratio 2:3
Since area varies as the square of the circumference. their cross-sectional
areas are in the ratio of 2²:3² or 4:9, and since the rate at which water flows
through a unit cross-sectional area is same for all the three pipes, pipe B's
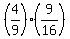
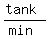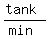filling rate is 4%2F9ths of C's filling rate or %284%2F9%29%289%2F16%29%28tank%29%2F%28min%29 or 1%2F4%28tank%29%2F%28min%29.

Pipes B and C fill another tank twice as big as the first.
how long will it take for B and C to fill the second tank?
B's and C's combined filling rate is 

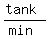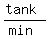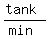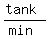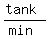1%2F4%28tank%29%2F%28min%29+9%2F16%28tank%29%2F%28min%29 = 4%2F16%28tank%29%2F%28min%29+9%2F16%28tank%29%2F%28min%29 = 13%2F16%28tank%29%2F%28min%29 
 
Since the second tank is twice as big as the first tank (I assume in volume),
it is the same as if they filled 2 tanks the size of the tank that A fills.

We will borrow the equation (rate)(time)=(distance covered), from motion
problems, by replacing "distance covered" by "tanks filled". 

Let t = the number of minutes it will take B and C to fill 2 tanks:

Then (B and C's combined rate)(time) = (2 tanks) 


       13%2F16t = 2

Multiply both sides by 16%2F13
    
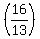          t = 2·%2816%2F13%29
          t = 32%2F13 = 2.461538462 or about 2.5 minutes.

Edwin